Implement these two methods in programs (java), and use each of these to approximately integrate the function f(x) = sin(x) over the interval [0, 1], using successively the following values of M: M = 2, 4, 8, 16, . For each of these values of M print the error, i.e., the absolute value of the difference between the approximation and the known exact value of the integral. Make sure to represent to sufficient precision in your program!

Furthermore, for each of the two methods, determine the smallest value of M for which the error is less than 107 . How many function evaluations are required in each of these two cases?

Can you describe the observed behavior of the error? In particular, for each of the two methods, can you say approximately how the error depends on h ? More specifically, it is known that the errors will be approximately proportional to h p , where p is an integer that depends on the method. Can you tell from the numerical results what p is for each of the two methods? Also can you explain what happens to the error when M gets very large.

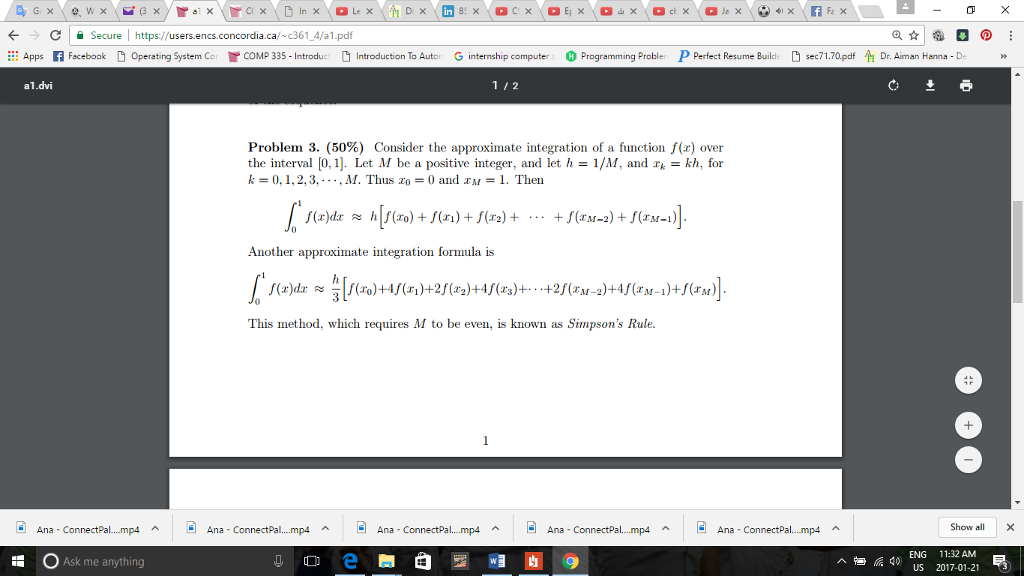
Secure h ps://us ers encs concordia ca c361 4/a Apps R Facebook D operating system Cor r COMP 335 Introd D Introduction To Auto G internship computers Programming problen P Perfect Resume Builde D sec71.70pdf A Dr. Aiman Hanna De al dvi Problem 3. (50%) Consider the approximate integration of a function f(z) over the interval 0,1 et M be a positive integer, and let h 1/M, and kh, for M. Thus zo 0 and 1. Then 0,1,2,3 f( f aCM a M. Another approximate integration formula is +2. f(z M-2 This method, which requires M to be even, is known as Simpson's Rule. Ana nectPal A lE Ana ConnectPa Ana ConnectP A 4 Ana Connect Pal Con n Ana ConnectPa mp4 A Show all X A 40 ENG 32 AM US 2017-01-2 Ask me anything