Implement versions of Eulers Method and the Explicit Trapezoid Method in Matlab to take four inputs: Int, y₀, N, f and outputs t, y.

Int is the left and right endpoint of the interval.

y₀ is the value of the solution at Int(1).

N is the number of iterations of the method.

f is an inline function representing the right hand side of the differential equation, i.e. y' = f(t, y).

3. This problem uses the floor function, also known as the greatest integer function, denoted by 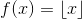. It simply outputs the integral part of the input. For a real number 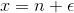, with 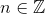and 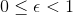, we have

.

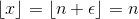So 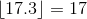, 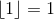and 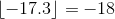. It is implemented in Matlab by floor. Consider the initial value problem

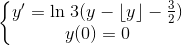
(a) Show that 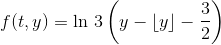is not Lipschitz in y. (Hint: in fact, its not even continuous. Simply show that for do this by choosing 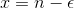for 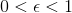and let .)

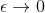(b) Show that 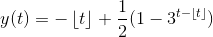is a solution to the initial value problem (i.e., show that it satisfies the differential equation and initial condition for most values of t the derivative will be fairly easy to compute, but you may have to think a little bit when t ? Z.) (c) Use your implementations of the Euler and trapezoid methods to get numerical solutions for t ? [0, 8]. Calculate the maximum errors for h = 1/10, 1/50, 1/100 and h = 1/500 and give your results in a table with two columns.