Implicit regularization:

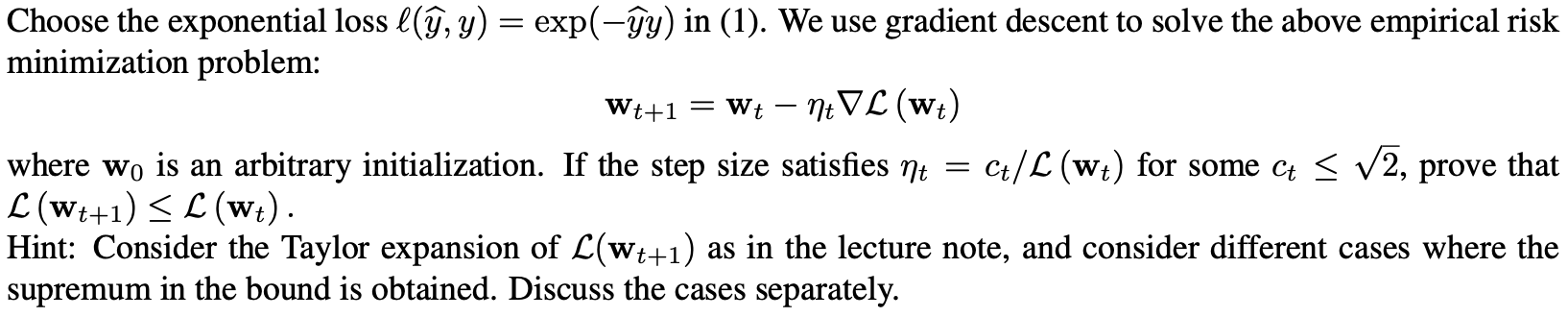
Problem Setting for Question Assume we have a training dataset { (Xi, yi) )i=1, where x; E Rd is the input vector and yi E { +1 } is the label, i = 1, ..., n. For a linear model f (x) = w x with parameter w E Rd, consider the following empirical risk minimization problem n L(W) := Ce((w, xi), yi) (1) i=1Choose the exponential loss \"if, y) = exp(y) in (1). We use gradient descent to solve the above empirical risk minimization problem: Wt+1 = Wt ntv (Wt) where we is an arbitrary initialization. If the step size satises m = ct/LI (wt) for some Ct g , prove that L (Wt+1) S (Wt) . Hint: Consider the Taylor expansion of (wt+1) as in the lecture note, and consider different cases where the supremum in the bound is obtained. Discuss the cases separately