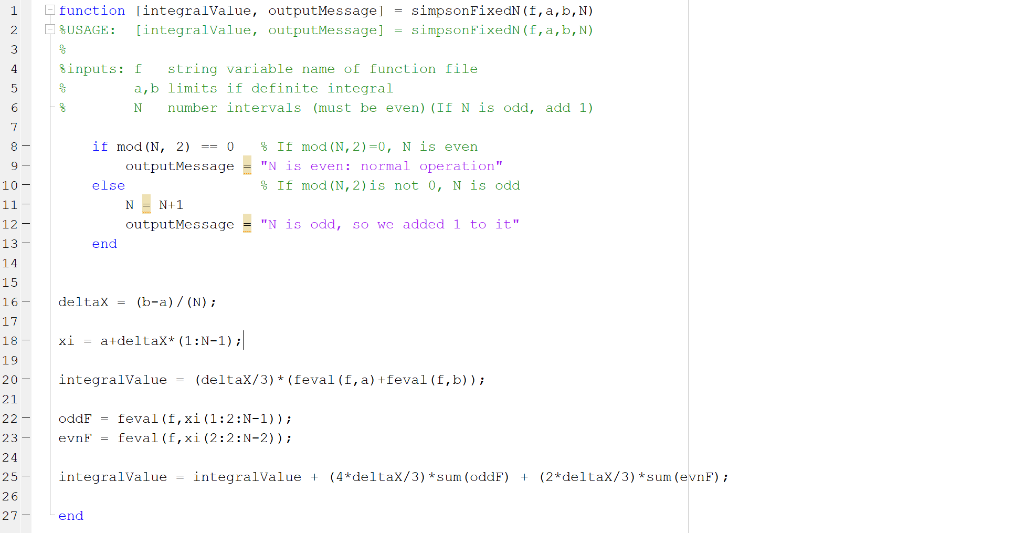
Improve vour Simpson's rule function. The function call should be function [integralValue] simpsonsRule (f,a,b, tolInt) In the improved version, you must compute Simpson's approximations for increasin,g values of N until the error between the true integral and the Simpson's approximation are within TolInt of each other. This problem requires you to estimate the error using the Simpson's error formula. The output value integralValue is the Simpson's rule integral approximation 1. Using an error tolerance of 10*, apply this function to the integrals bSIn(r) To make this computation, create a single "driver" script that runs the simpsonsRule function for each integral make sure your driver script will displav the results when I run it 2. Explore the fourth-order nature of the Simpson's approximation through repeated computation using your simpsonFixedN function. To do this, compute the error between your Simpson's approximation and |8x'dr , an integral you can compute exactly, for N-10,20,40,80,160. Create a MATLAB script that evaluates these Simpsons' computations and plots the error vs. Ar for these five points. What does the nlot look like function %USAGE : [integralValue, [integralValue, fina1N] finalN] simpson ( f , a,b, tol Int) simpson(f,a,b, tol!nt) = 2 3 4 = inputs: f string variable name of function file (use simpsonFixe limits if definite integra.l 6 TolInt convergence tolerance 7 currentError1010 9 10 if mod (N, 2) else N N+1 end 0; 12 13 14 15 16 17 18 19 20 21 currentIntegral -simpsonFixedN (f, a,b, N); while (currentError >- tolInt) N = N+2; newIntegral- simpsonFixedN (f, a, b,N); currentError abs (currentIntegral-newIntegral); currentIntegral-newIntegral; 23 2 4 25 26 27 28 end integra!Value = currentintegral finalN = N end tunction 1 2 integralValue, outputMessagesimpsonFixedN (t,a,b, N) [integra 1 Value, output-Message ]=simpsonFixedn(f,a,b,N) %USAGE : inputs:string variable name of unction Tile a,b limits if dcfinite intcgral N umber intervals (must be even) (If N is odd, add 1) it mod (N, 2) 0 % If mod (N,2)-0, N is even -- 9 output.Message- "N is even: normal ope ration" 10 - else % If mod (N, 2) s not 0, N is odd 12 - 13 1 4 15 16-deltaX (b-a) (N) 17 18 outputMcssage"N is odd, so we added 1 to it" end xi - aideltaX" (1: N-1); integralValue(deltaX/3)* (feval (f,a) feval (f,b)) oddF = feval ( f , xi (1 :2 :N-1)); 20 21 22- 23 24 25 26 27 evnt. feval (f, (2 :2 : N-2)); integralValue-integralValu(4*deltaX/3) sum (oddF)(2*delLaX/3) *sum (evnF) end Improve vour Simpson's rule function. The function call should be function [integralValue] simpsonsRule (f,a,b, tolInt) In the improved version, you must compute Simpson's approximations for increasin,g values of N until the error between the true integral and the Simpson's approximation are within TolInt of each other. This problem requires you to estimate the error using the Simpson's error formula. The output value integralValue is the Simpson's rule integral approximation 1. Using an error tolerance of 10*, apply this function to the integrals bSIn(r) To make this computation, create a single "driver" script that runs the simpsonsRule function for each integral make sure your driver script will displav the results when I run it 2. Explore the fourth-order nature of the Simpson's approximation through repeated computation using your simpsonFixedN function. To do this, compute the error between your Simpson's approximation and |8x'dr , an integral you can compute exactly, for N-10,20,40,80,160. Create a MATLAB script that evaluates these Simpsons' computations and plots the error vs. Ar for these five points. What does the nlot look like function %USAGE : [integralValue, [integralValue, fina1N] finalN] simpson ( f , a,b, tol Int) simpson(f,a,b, tol!nt) = 2 3 4 = inputs: f string variable name of function file (use simpsonFixe limits if definite integra.l 6 TolInt convergence tolerance 7 currentError1010 9 10 if mod (N, 2) else N N+1 end 0; 12 13 14 15 16 17 18 19 20 21 currentIntegral -simpsonFixedN (f, a,b, N); while (currentError >- tolInt) N = N+2; newIntegral- simpsonFixedN (f, a, b,N); currentError abs (currentIntegral-newIntegral); currentIntegral-newIntegral; 23 2 4 25 26 27 28 end integra!Value = currentintegral finalN = N end tunction 1 2 integralValue, outputMessagesimpsonFixedN (t,a,b, N) [integra 1 Value, output-Message ]=simpsonFixedn(f,a,b,N) %USAGE : inputs:string variable name of unction Tile a,b limits if dcfinite intcgral N umber intervals (must be even) (If N is odd, add 1) it mod (N, 2) 0 % If mod (N,2)-0, N is even -- 9 output.Message- "N is even: normal ope ration" 10 - else % If mod (N, 2) s not 0, N is odd 12 - 13 1 4 15 16-deltaX (b-a) (N) 17 18 outputMcssage"N is odd, so we added 1 to it" end xi - aideltaX" (1: N-1); integralValue(deltaX/3)* (feval (f,a) feval (f,b)) oddF = feval ( f , xi (1 :2 :N-1)); 20 21 22- 23 24 25 26 27 evnt. feval (f, (2 :2 : N-2)); integralValue-integralValu(4*deltaX/3) sum (oddF)(2*delLaX/3) *sum (evnF) end