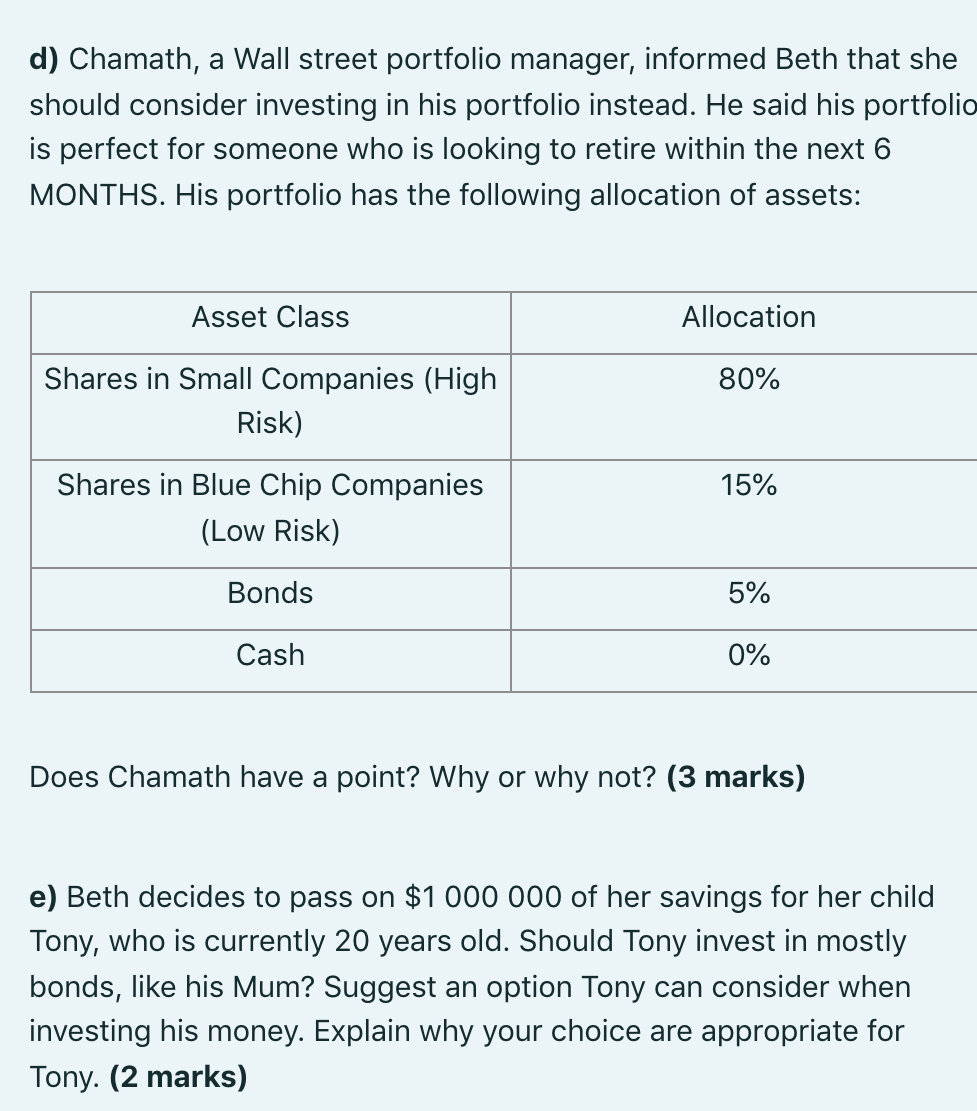
In 2015 Beth purchased a 15-year, 2.75% p.a. semi-annual paying coupon bond with a Face Value (FV) of $3 000 000, as she was attracted by the fixed income stream in order to fund her retirement expenses. a) What is the price of this bond in 2020 (10 years remaining) at a current market yield of 0.30% p.a.? (3 marks) Show formula, variables, calculation and a concluding statement in your response. b) Is Beth's coupon bond currently selling at a premium, par or discount? Describe the relationship between bond prices and interest rates. (2 marks) c) Beth decided to sell the bond from part a) and is considering her investment options. A friend suggested that she invests the proceeds by shares. Explain two advantages shares have compared to bonds. (2 marks) d) Chamath, a Wall street portfolio manager, informed Beth that she should consider investing in his portfolio instead. He said his portfolio is perfect for someone who is looking to retire within the next 6 MONTHS. His portfolio has the following allocation of assets: Asset Class Allocation 80% Shares in Small Companies (High Risk) 15% Shares in Blue Chip Companies (Low Risk) Bonds 5% Cash 0% Does Chamath have a point? Why or why not? (3 marks) e) Beth decides to pass on $1 000 000 of her savings for her child Tony, who is currently 20 years old. Should Tony invest in mostly bonds, like his Mum? Suggest an option Tony can consider when investing his money. Explain why your choice are appropriate for Tony. (2 marks) 1. Simple interest 2.6 Number of time periods at compound interest I= simple interest; P = principal; r = interest rate p.a.; t = time in terms of a year; FV = future value; PV = present value; FV Ln PV 1.1 Calculation of simple interest: n = Ln(1+r) I= Pxrxt Future value of principal at simple interest: 1.2 3. Annuities FV=PV (1+rxt)) Present value at simple interest: 1.3 A=cash flow received/paid; FV=future value; PV=present value; r=interest rate per compounding period; n=number of periods; Ordinary Annuities FV PV =FV (1+(rxt) 'or PV=- (1+(rxt)) Yield at simple interest: 3.1 1.4 Present value of n payments of A at interest rate : 1 FV r = --X t PV Number of time periods at simple interest: [1-(1+r) PV = A 1.5 3.2 Future value of n payments of A at interest rate : FV PV (1+r)"-1 FV=A[+)" = 2. Compound interest 3.3 Calculation of cash flow (A) when the present value is known: FV=future value; PV=present value; r-interest rate per compounding period; n=number of periods; m=number of compounding periods in one year; is effective rate p.a.; = nominal rate p.a. PV A= 2.1 Future value of principal at compound interest: [1-(1+r) FV =PV (1+r)" 3.4 Calculation of cash flow (A) when the future value is known: 2.2 Present value at compound interest: FV A= (1+r)" -1 FV PV =FV (1+r)" or PV =- (1+r)" Effective annual interest rate when nominal interest rate is known: ( * ) 2.3 Annuity Due 3.5 nom Present value of an annuity due: i = 1+ -1 m Nominal annual interest rate when effective interest rate is known: -) 2.4 [1-(1+r)" PV = A 110-4?\"]}+r) ) From = ml mi[(1 (1+i)%m - 1 -1) 3.6 Future value of an annuity due: 2.5 Yield at compound interest: (1+r)1 FV=d[0*7*-"]=> A (1+r) 1/ -- * r = FV PV -1 3.7 Calculation of cash flow (A) when the present value is known: 4.5 Risk measurement using probabilities: * 19-007" PV A= [[1 (1+r)""] (1 + r) (- = (1-1 - r)? Pr ) 4.6 Return of a portfolio: 3.8 Calculation of cash flow (A) when the future value is known: , - = A= [1+79-4}+ FV (1 + r)"-1] (1+r) r Perpetuity re-portfolio return; w;= weight of assetj in the portfolio; r return of asset i Search documents and file 4.7 Beta Coeffic 0 1 Bi = Pmkt, i * Omkt B-Beta Coefficient; Px-Correlation between the market and stock i; ; standard deviation (risk) of stock i; Omkr standard deviation (risk) of the market. 3.9 Perpetuity - when the constant cash flow (A) is known: PV = A r 4. Risk and Return 4.8 Beta of a portfolio: , -, , Risk and Returns using Historical Data CFxr-income (or dividend) received during the holding period; PEND =price at the end of holding period; Peegi-price at start of holding period; r, return at timet; nnumber of returns; a, standard deviation (risk) of returns, B, - portfolio Beta; w; = weight of assetj in the portfolio: B -betu of asset i. 4.1 Historical return with income: 5. Bond Pricing CFHp+(PEND-PBEGIN) rt = PBEGIN 5.1 Present value of a coupon paying bond [PV of coupon payments + PV of face value: Formula 3.1+Formula 2.2] 4.2 Expected return using historical returns: 1-(1+r) PV = A -44-479 FV + (1+r)" E(R)= r = n Risk measurement using historical returns: 4.3 11 (; -;-) ? 6. Share Valuation Value of a share using dividend valuation models: A 6.1 (Zero Growth): V = k 1 n-1 D 6.2 (Constant Growth): V = k-8 Risk and Returns using Probabilities r;=return for outcome i; Pre probability of return i occurring; n = numbe of returns; 6,-standard deviation (risk) of returns; 4.4 Expected return using probabilities: A-annual constant dividend payment; D=D. (1+g); k=required rate of return; g =constant rate of growth in dividends. E(R) = r=