Question: in (5) LinkedIn x )TalentEd Hire - Edit References x (61,760 unread) - debra.kelly38( x 9 Exam: 01.09 Geometry Foundati x + C a learn.flvs.net/educator/student/examform.cgi?cnewlon2*laurenkkelly01*sit=xVjtvSCN81Bzw*5631*0009**passedonce**#

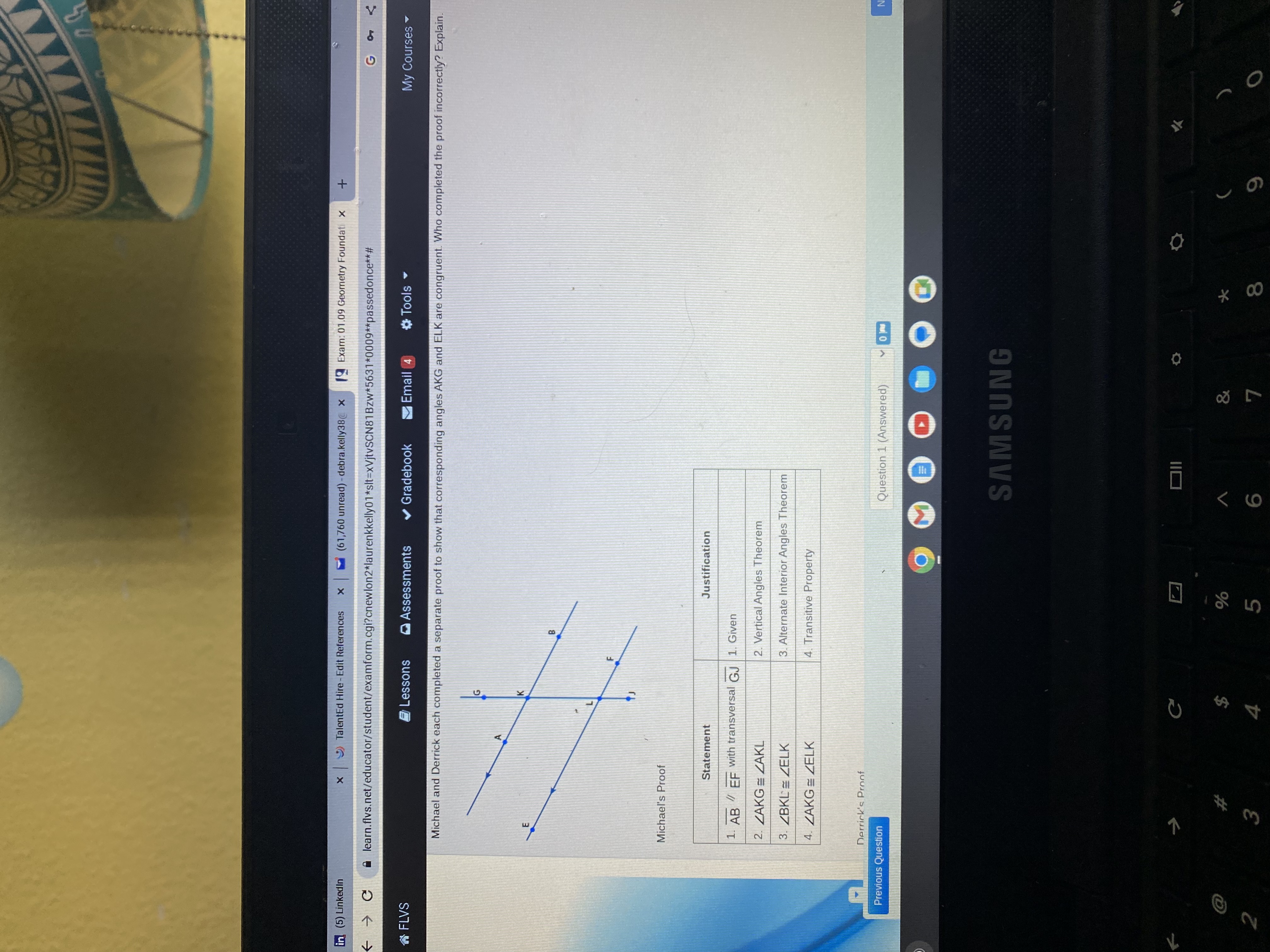
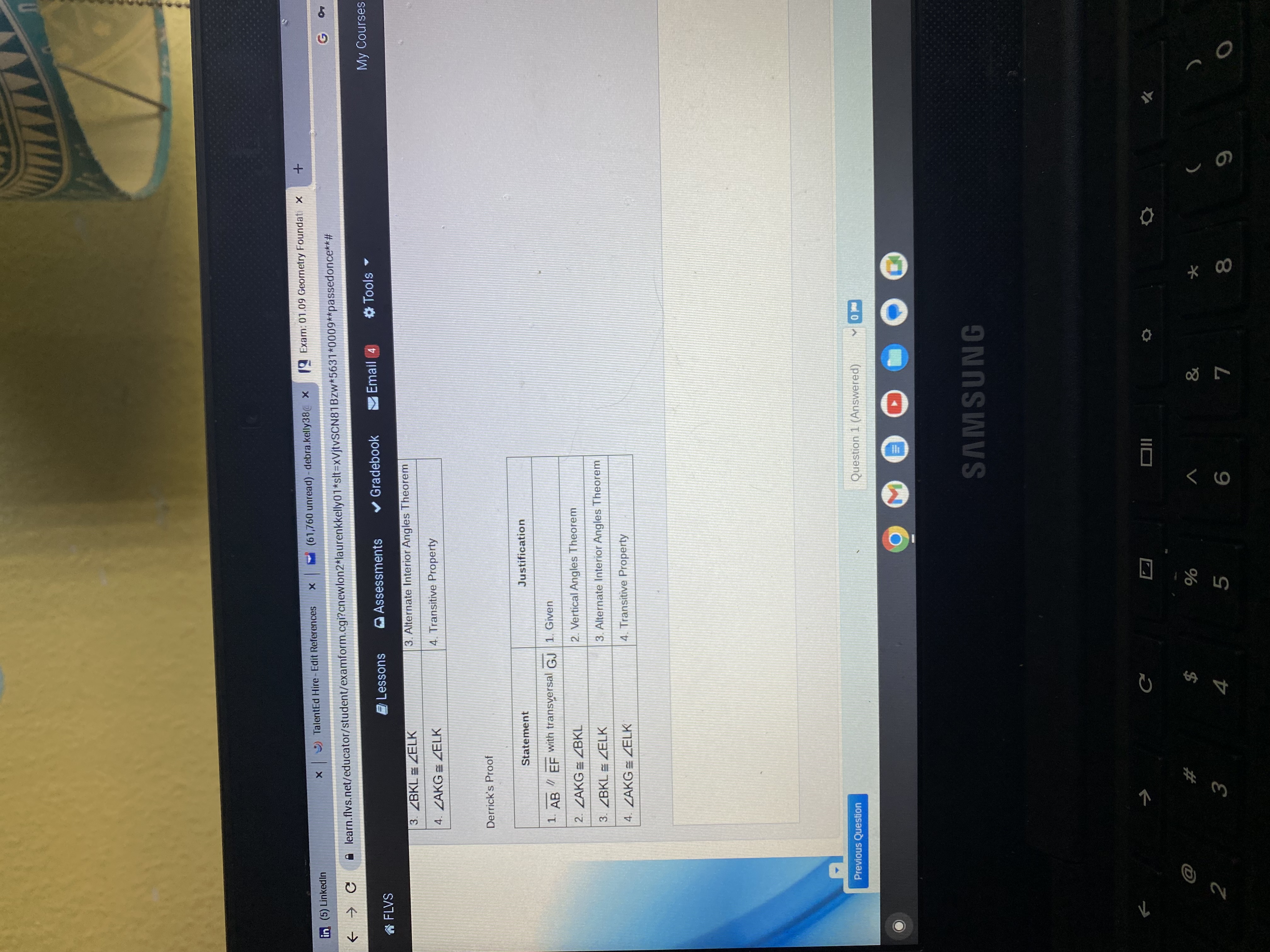
in (5) LinkedIn x )TalentEd Hire - Edit References x (61,760unread) - debra.kelly38( x 9 Exam: 01.09 Geometry Foundati x + C

in (5) LinkedIn x )TalentEd Hire - Edit References x (61,760 unread) - debra.kelly38( x 9 Exam: 01.09 Geometry Foundati x + C a learn.flvs.net/educator/student/examform.cgi?cnewlon2*laurenkkelly01*sit=xVjtvSCN81Bzw*5631*0009**passedonce**# Go FLVS Lessons Assessments Gradebook Email 4 # Tools My Courses Michael and Derrick each completed a separate proof to show that corresponding angles AKG and ELK are congruent. Who completed the proof incorrectly? Explain. Michael's Proof Statement Justification 1. AB / EF with transversal GJ 1. Given 2. LAKG = ZAKL 2. Vertical Angles Theorem 3. LBKL = ZELK 3. Alternate Interior Angles Theorem 4 . LAKG = ZELK 4. Transitive Property Derrick's Proof Previous Question Question 1 (Answered) 1 0m SAMSUNG OII $ & K 3 4 5 6 7 8 Ox TalentEd Hire -Edit References x (61,760 unread) - debra.kelly38@ x 19 Exam: 01.09 Geometry Foundati x + in (5) Linkedin C a learn.flvs.net/educator/student/examform.cgi?cnewlon2*laurenkkelly01*sit=xVjtvSCN81Bzw*5631*0009**passedonce**# FLVS Lessons Assessments Gradebook Email 4 # Tools My Courses 3. ZBKL = ZELK 3. Alternate Interior Angles Theorem 4. ZAKG = ZELK 4. Transitive Property Derrick's Proof Statement Justification 1. AB / EF with transversal GJ |1. Given 2. LAKG = ZBKL 2. Vertical Angles Theorem 3. LBKL = ZELK 3. Alternate Interior Angles Theorem 4. ZAKG = ZELK 4. Transitive Property Previous Question Question 1 (Answered) 0 O SAMSUNG 110 @ $ 2 3 4 5 6 8 O

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Q:

Whereas, MCPS Manufacturing costs of products sold NPMC Non-Product Manufacturing costs MCFP Manufacturing cost of the production This is the complete question. There is no additional information...

Q:

MANAGEMENT (HARLEY DAVIDSON) QUESTION 1 Conduct an environmental analysis for Harley Davidson Based on the following results: TABLE 1: FINANCIAL RATIO ANALYSIS (MARCH 2004) Company Sector S&P 500...

Q:

Calculate the tier 1 to risk-weighted assets and tier 1 to total assets ratios, and then categorize New River National Bank as Well Capitalized , Adequately Capitalized , Undercapitalized ,...

Q:

Practice the concept of segmentation and buyer personas with this in-class activity. The Target Market Segment Research the typical customer who visit Panorama Ski Resort outside Invermere, BC. What...

Q:

6 (6) WhatsApp X D2L 2. Mid Term Exam - 22 X Question 11 - HRPD 70 X | Chegg.com X C Get Homework Help W X in (15) Feed | Linkedin X + C D...

Q:

Macro quiz.. Problem 1. (Consumer Choice) Lionel watches movies z, while drinking beer, 23. His utility function from consuming the two types of goods is given by U(21. 12) = 5In(21) + 10in(zz) a)...

Q:

Show alll the steps Problem 3. (Technology) Suppose a producer has access to the technology given by the Cobb-Douglass production function y = 3K1 14. a) What can you say about the returns to scale...

Q:

I need help creating an bio for an underground utility contractor with the following information i want the experience and skills listed and correct terminology 6:30 ( 51m .............. 794 Q Elite...

Q:

X S TEST 2: PROJECT INITIATION | Sc X 9 linkedin login - Search x in Feed | LinkedIn x Your In Progress Content X tps://app.schoology.com/assignment/6244496961/assessment COURSES GROUPS RESOURCES...

Q:

:Help me answer the following questions, thanks. Starbucks Corporation January 2017. After sitting through another long executive meeting, Starbucks chairman and CEO Howard Schultz, now in his...

Q:

ED Bb Discussic X to Mail - Bre x 5 WileyPLU X Calendar X Lead: Ric X Lead: Mic X Lead: Zul X Lead: Jus X Lead: Mr X Lead: B C A edugen.wileyplus.com/edugen/student/mainfr.uni Apps Salesforce -...

Q:

Is this practice ethical?

Q:

1. In the bronsted-lowry definition of acids and bases: an acid (a) Is a proton acceptor (c) Is a proton donor (b) Corrodes metals (d) Form stable hydrogen bonds.

Q:

Any asset held for future use or sale is known as inventory. True False

Q:

On 1 March 2007 DB Limited issued R560 000 15% debentures at R98. The debentures were to be redeemed at par in four equal annual payments starting 28 February 2010. Required: Journalise the above...