In a research, students reported their typical time to run a mile, and whether or not they were an athlete. Suppose we want to know if the average time to run a mile is different for athletes versus non-athletes. This involves testing whether the sample means for mile time among athletes and non-athletes in your sample are statistically different (and by extension, inferring whether the means for mile times in the population are significantly different between these two groups). We can use an Independent SamplestTest to compare the mean mile time for athletes and non-athletes.

In the sample data, we will use two variables:AthleteandMileMinDur. The variableAthletehas values of either "0" (non-athlete) or "1" (athlete). It will function as the independent variable in this T test. The variableMileMinDuris a numeric duration variable (h:mm:ss), and it will function as the dependent variable. In SAS, the output look like this:

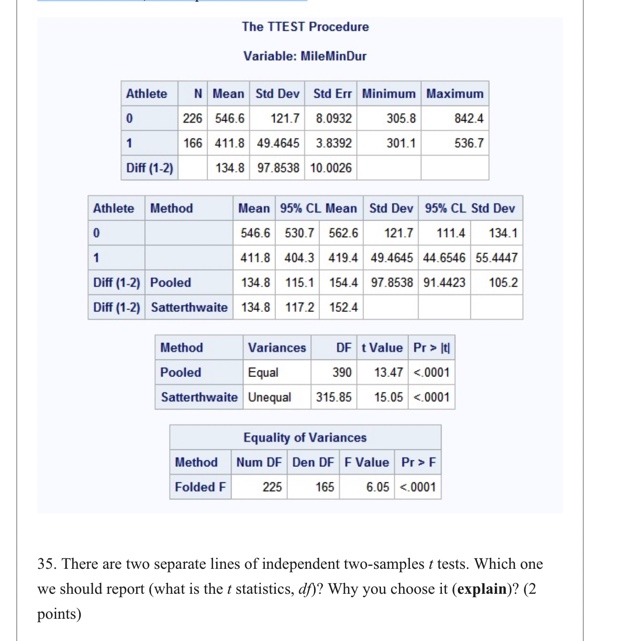
The TTEST Procedure Variable: MileMinDur Athlete N Mean Std Dev Std Err Minimum Maximum 226 546.6 121.7 8.0932 305.8 842.4 1 166 411.8 49.4645 3.8392 301.1 536.7 Diff (1-2) 134.8 97.8538 10.0026 Athlete Method Mean 95% CL Mean Std Dev 95% CL Std Dev 546.6 530.7 562.6 121.7 111.4 134.1 411.8 404.3 419.4 49.4645 44.6546 55.4447 Diff (1-2) Pooled 134.8 115.1 154.4 97.8538 91.4423 105.2 Diff (1-2) Satterthwaite 134.8 117.2 152.4 Method Variances DF t Value Pr > It) Pooled Equal 390 13.47 <.0001 satterthwaite unequal equality of variances method num df den f value pr> F Folded F 225 165 6.05 <.0001 there are two separate lines of independent two-samples tests. which one we should report is the statistics d why you choose it points>