In a workshop, there are 25 tasks that needs to be done by 6 employees. To perform each task, only one employee is required. These employees have different levels of expertise in performing these task. Therefore, as indicated in Table 1, the duration of performing each task depend on the employee that is going to do the task. Moreover, employees have different preferences for doing the different tasks. The level of their preferences is measured by a number between 1 to 10. The details of employees preferences for performing the task are given in Table 2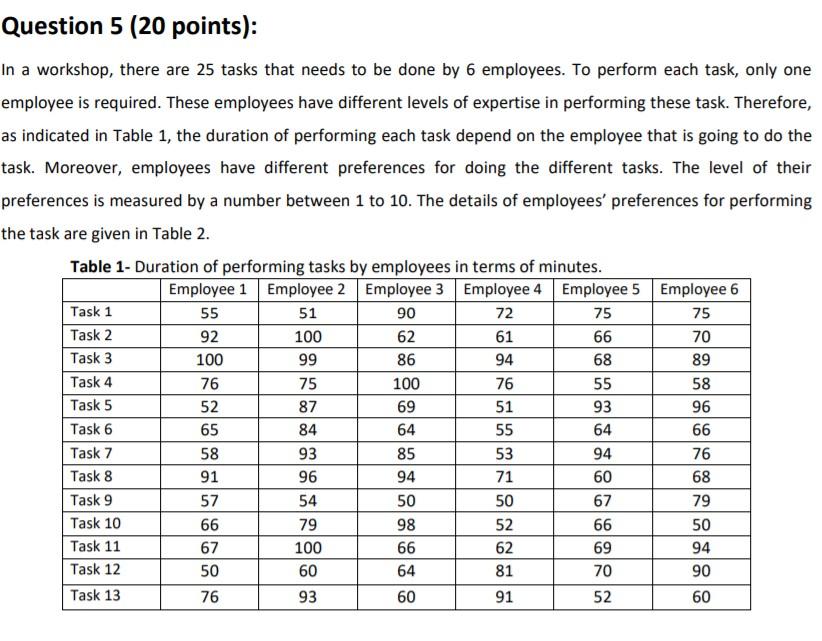

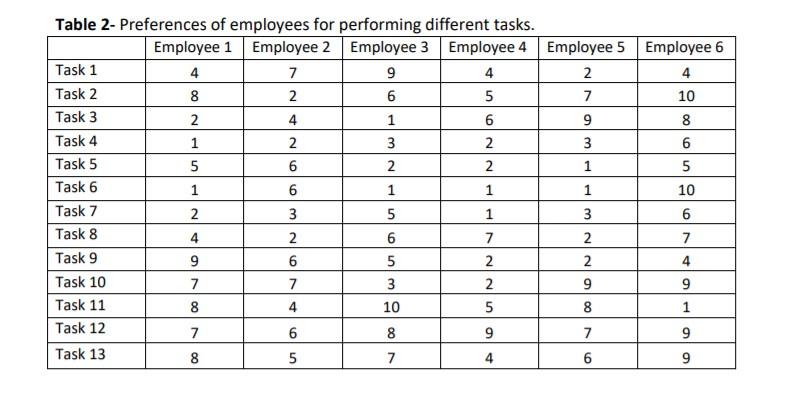
Question 5 (20 points): In a workshop, there are 25 tasks that needs to be done by 6 employees. To perform each task, only one employee is required. These employees have different levels of expertise in performing these task. Therefore, as indicated in Table 1, the duration of performing each task depend on the employee that is going to do the task. Moreover, employees have different preferences for doing the different tasks. The level of their preferences is measured by a number between 1 to 10. The details of employees' preferences for performing the task are given in Table 2. Table 1- Duration of performing tasks by employees in terms of minutes. Employee 1 Employee 2 Employee 3 Employee 4 Employee 5 Employee 6 Task 1 55 51 90 72 75 75 Task 2 92 100 62 61 66 70 Task 3 100 99 86 94 68 89 Task 4 76 75 100 76 55 58 Task 5 69 51 93 96 Task 6 65 84 64 55 64 66 Task 7 58 93 85 53 94 76 Task 8 96 94 71 Task 9 54 50 50 67 79 Task 10 66 98 52 Task 11 67 100 66 62 69 94 Task 12 50 60 64 81 70 90 Task 13 91 52 52 87 60 68 91 57 79 66 50 76 93 60 60 Employee 6 4 10 Nw Table 2- Preferences of employees for performing different tasks. Employee 1 Employee 2 Employee 3 Employee 4 Employee 5 Task 1 4 7 9 4 2 Task 2 8 2 6 5 7 Task 3 2 4 1 6 9 Task 4 1 2 2 3 Task 5 5 6 2 1 Task 6 1 6 1 1 1 Task 7 2 3 5 1 3 Task 8 4 2 6 7 2 Task 9 9 6 5 2 2 Task 10 7 7 3 2 9 Task 11 8 4 10 5 8 Task 12 7 6 8 9 7 Task 13 8 5 7 6 6 6 00 ON 6 5 10 6 7 4 9 1 Nw 9 9 8 5 4 Part a) write a mathematical programming model to help the manager assign tasks to employees such that all tasks are performed, each employee does not work more than 350 minutes, and the total preferences of all employees with respect to the assigned tasks are maximized. (6 points) Part b) How would you modify the model to ensure that at most 3 task is assigned to each employee? (2 points) Part c) How would you modify the model to ensure that the total preference of each employees with respect to assigned jobs will be more than 40? (2 points) Part d) How would you modify the model to ensure that if task 1 is assigned to employee 3 then task 3 must be assigned to employee 6? (2 points) Part e) How would you modify the model to ensure that, among tasks 4, 7, 9, 11, and 13, at most 3 of them can be assigned to employee 4? (2 points) Part f) How would you modify the model to ensure that if tasks 3 and 8 are assigned to employee 2, then tasks 5 and 6 are assigned to employee 4? (3 points) Part g) How would you modify the model to ensure that if the total preference of employee 1 is more than 30, then the total preference of employee 3 must be more than 40? (3 points) Question 5 (20 points): In a workshop, there are 25 tasks that needs to be done by 6 employees. To perform each task, only one employee is required. These employees have different levels of expertise in performing these task. Therefore, as indicated in Table 1, the duration of performing each task depend on the employee that is going to do the task. Moreover, employees have different preferences for doing the different tasks. The level of their preferences is measured by a number between 1 to 10. The details of employees' preferences for performing the task are given in Table 2. Table 1- Duration of performing tasks by employees in terms of minutes. Employee 1 Employee 2 Employee 3 Employee 4 Employee 5 Employee 6 Task 1 55 51 90 72 75 75 Task 2 92 100 62 61 66 70 Task 3 100 99 86 94 68 89 Task 4 76 75 100 76 55 58 Task 5 69 51 93 96 Task 6 65 84 64 55 64 66 Task 7 58 93 85 53 94 76 Task 8 96 94 71 Task 9 54 50 50 67 79 Task 10 66 98 52 Task 11 67 100 66 62 69 94 Task 12 50 60 64 81 70 90 Task 13 91 52 52 87 60 68 91 57 79 66 50 76 93 60 60 Employee 6 4 10 Nw Table 2- Preferences of employees for performing different tasks. Employee 1 Employee 2 Employee 3 Employee 4 Employee 5 Task 1 4 7 9 4 2 Task 2 8 2 6 5 7 Task 3 2 4 1 6 9 Task 4 1 2 2 3 Task 5 5 6 2 1 Task 6 1 6 1 1 1 Task 7 2 3 5 1 3 Task 8 4 2 6 7 2 Task 9 9 6 5 2 2 Task 10 7 7 3 2 9 Task 11 8 4 10 5 8 Task 12 7 6 8 9 7 Task 13 8 5 7 6 6 6 00 ON 6 5 10 6 7 4 9 1 Nw 9 9 8 5 4 Part a) write a mathematical programming model to help the manager assign tasks to employees such that all tasks are performed, each employee does not work more than 350 minutes, and the total preferences of all employees with respect to the assigned tasks are maximized. (6 points) Part b) How would you modify the model to ensure that at most 3 task is assigned to each employee? (2 points) Part c) How would you modify the model to ensure that the total preference of each employees with respect to assigned jobs will be more than 40? (2 points) Part d) How would you modify the model to ensure that if task 1 is assigned to employee 3 then task 3 must be assigned to employee 6? (2 points) Part e) How would you modify the model to ensure that, among tasks 4, 7, 9, 11, and 13, at most 3 of them can be assigned to employee 4? (2 points) Part f) How would you modify the model to ensure that if tasks 3 and 8 are assigned to employee 2, then tasks 5 and 6 are assigned to employee 4? (3 points) Part g) How would you modify the model to ensure that if the total preference of employee 1 is more than 30, then the total preference of employee 3 must be more than 40? (3 points)