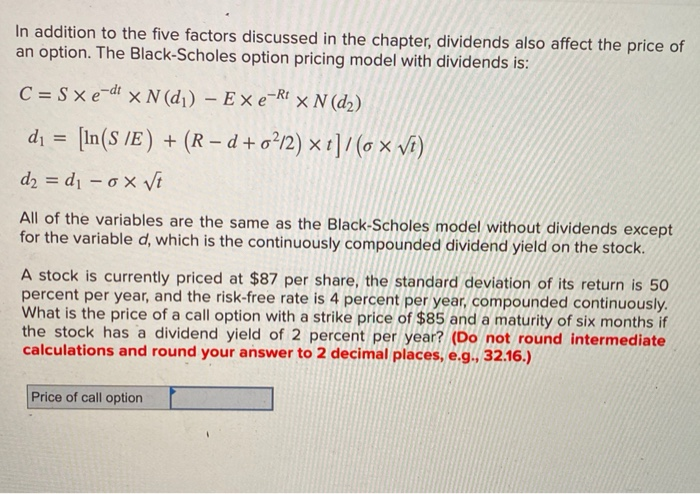
In addition to the five factors discussed in the chapter, dividends also affect the price of an option. The Black-Scholes option pricing model with dividends is: C = Sx e-dt x N(d) Ex e-Rt X N (d) d = [In(S IE) + (R d+o2/2) xt]/(o X Vi) d2 = di - OxVt All of the variables are the same as the Black-Scholes model without dividends except for the variable d, which is the continuously compounded dividend yield on the stock. A stock is currently priced at $87 per share, the standard deviation of its return is 50 percent per year, and the risk-free rate is 4 percent per year, compounded continuously. What is the price of a call option with a strike price of $85 and a maturity of six months if the stock has a dividend yield of 2 percent per year? (Do not round intermediate calculations and round your answer to 2 decimal places, e.g., 32.16.) Price of call option