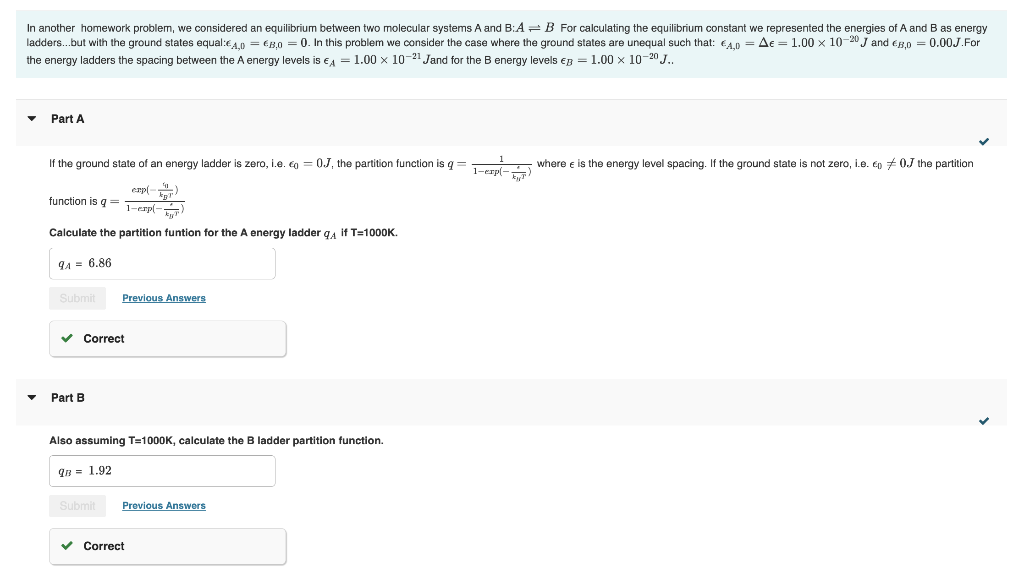
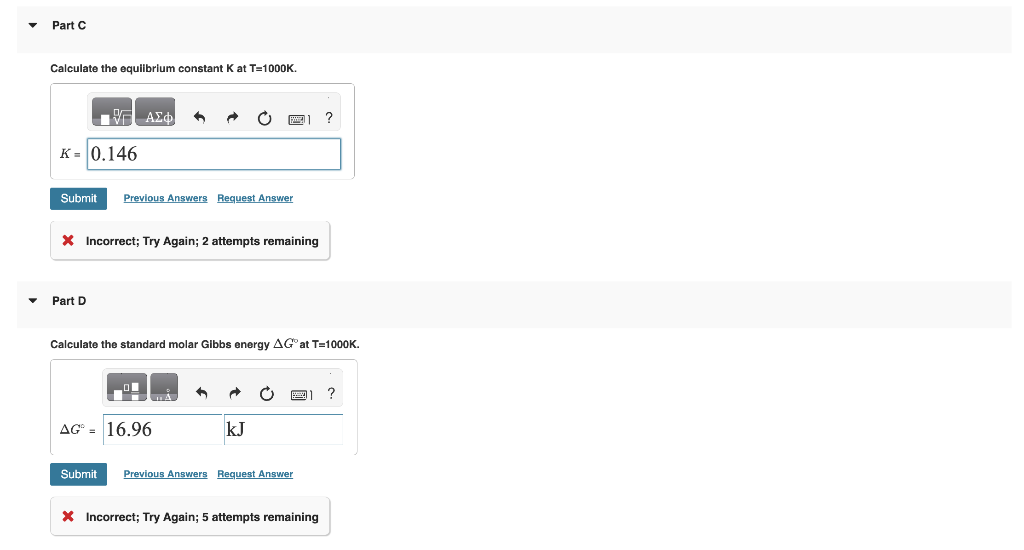
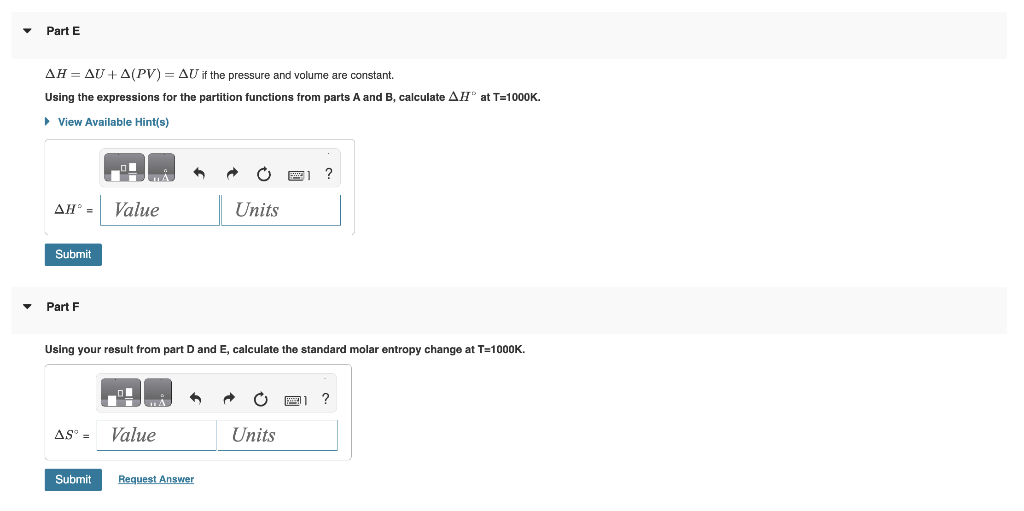
In another homework problem, we considered an equilibrium between two molecular systems A and B:AB For calculating the equilibrium constant we represented the energies of A and B as energy adders...but with the ground states equal: A,0=B,0=0. In this problem we consider the case where the ground states are unequal such that: A,0==1.001020J and B,0=0.00J. For the energy ladders the spacing between the A energy levels is A=1.001021J and for the B energy levels B=1.001020J.. Part A If the ground state of an energy ladder is zero, i.e. 0=0J, the partition function is q=1exp(kT)1 where is the energy level spacing. If the ground state is not zero, i.e. 0=0J the partition Calculate the partition funtion for the A energy ladder qA if T=1000K. Part B Also assuming T=1000K, calculate the B ladder partition function. Calculate the equilibrium constant K at T=1000K. * Incorrect; Try Again; 2 attempts remaining Part D Calculate the standard molar Gibbs energy G at T=1000K. * Incorrect; Try Again; 5 attempts remaining H=U+(PV)=U if the pressure and volume are constant. Using the expressions for the partition functions from parts A and B, calculate H at T=1000K. Part F Using your result from part D and E, calculate the standard molar entropy change at T=1000K. In another homework problem, we considered an equilibrium between two molecular systems A and B:AB For calculating the equilibrium constant we represented the energies of A and B as energy adders...but with the ground states equal: A,0=B,0=0. In this problem we consider the case where the ground states are unequal such that: A,0==1.001020J and B,0=0.00J. For the energy ladders the spacing between the A energy levels is A=1.001021J and for the B energy levels B=1.001020J.. Part A If the ground state of an energy ladder is zero, i.e. 0=0J, the partition function is q=1exp(kT)1 where is the energy level spacing. If the ground state is not zero, i.e. 0=0J the partition Calculate the partition funtion for the A energy ladder qA if T=1000K. Part B Also assuming T=1000K, calculate the B ladder partition function. Calculate the equilibrium constant K at T=1000K. * Incorrect; Try Again; 2 attempts remaining Part D Calculate the standard molar Gibbs energy G at T=1000K. * Incorrect; Try Again; 5 attempts remaining H=U+(PV)=U if the pressure and volume are constant. Using the expressions for the partition functions from parts A and B, calculate H at T=1000K. Part F Using your result from part D and E, calculate the standard molar entropy change at T=1000K