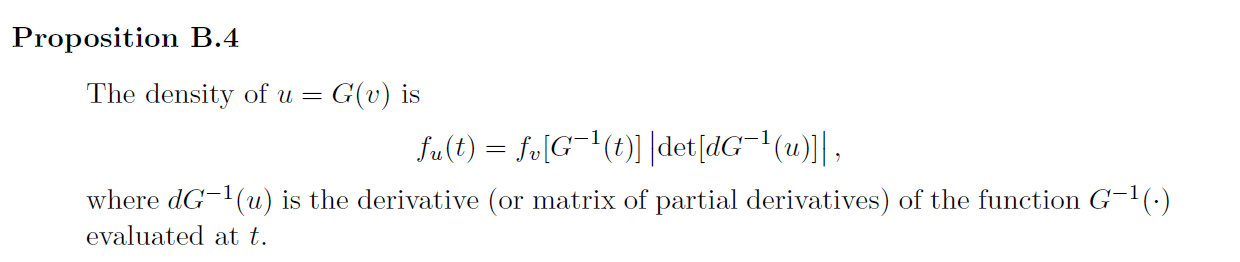
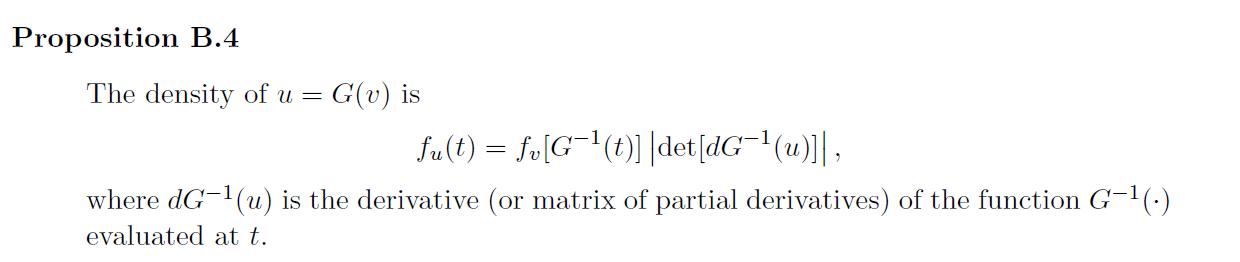
In binomial regression with r predictor variables, we have independent observations yildi~ Bin (Ni, 0i) and 0i = F(x;3). We need a prior on B. Rather than directly eliciting an r dimensional prior on S, we pick r predictor variable vectors {ch : h = 1, ...,r}, imagine the associated probabilities Oh = F(x, B), and elicit independent prior distributions on the Ohs. We typically use Oh no Beta (yh, Nh - yh ) regardless of the choice of the link function F-1. Let the function f(.) be the first derivative of the function F(.). Use Proposition B.4 again to derive the expression r P(B) x [IF(Th B)jun-1[1 - F(ahB)] Nn -yn-If(ichB). h=1 Then show that in the logistic link case, this expression reduces to r et P(B) x [F (ich B) lyn [1 - F(ahB)] Wh-uh, F(t) = 1+ et h=1Proposition B.4 The density of u = G(v) is fu(t) = fulG 1(t)] | det[dG-1(u)]], where dG-(u) is the derivative (or matrix of partial derivatives) of the function G-1(.) evaluated at t