In class, we discussed the structure of shocks when the shock heated gas radiates so efficiently that it returns to its preshock temperature over such a short distance that the shock can be considered isothermal. In this problem we consider how this situation is affected by a magnetic field tangent to the shock. The shock jump conditions are 

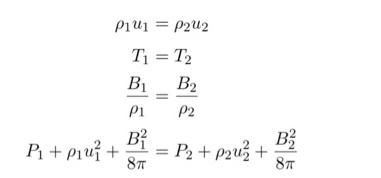1. From the jump conditions, derive and solve an equation for the compression ratio R = P2/pi in terms of the shock speed u1 and the upstream conditions. 

2. Recall that hydrodynamic shocks must be compressive R > 1 for entropy to increase across them. The same condition holds in this case. Find the shock speed u for which R = 1 (which is the minimum speed of a shock), and give a physical interpretation. 

3. Solve the equation you derived for R in Part 1 and take the limit u21 >> u2A1 C2. Compare the scaling of R with Mms in this case to the hydro- dynamic case with M > 1. Which is more compressive? Why? 

4. Find R for a hydrogen plasma with T = 10⁴K, B = 5μG, ni = 0.1 cm-3, uj = 50 km s-1.

= 22 P + pu + Ti = T2 B 1 B 8 B2 2 = P + p2u3 + B2 8