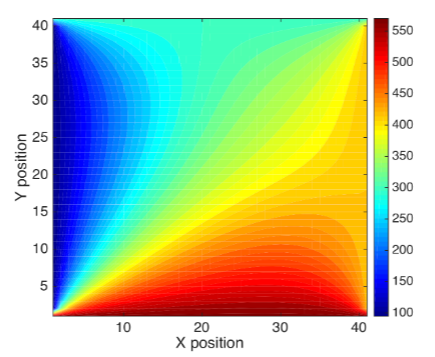
In class we have discussed a numerical approach for estimating a solution to the Energy Equation for 2-D, steady state conduction in a rectangular slab. Suppose we have a square domain, 40 cm on each side. The edge temperatures are maintained as follows: left side 95F, bottom 575F, right side 420F, top 300F. Use of computational software such as Mathematica/MATLAB is recommended for this assignment. The resulting temperature profile looks like this:

A) This time the material is placed on a heated surface, keeping the bottom temperature at a uniform 140F. The edge temperatures on the left, right, and top are kept a uniform temperatures of 100, 90, 70F, respectively. Prepare an appropriate contour plot as shown for this situation. What is the average temperature within the block and at the center of the square?

B) Now, suppose you insulate the top of this block, while the temperatures on bottom is the same. The temperature on the left and right side are increased to 120 and 105F, respectively. Prepare an appropriate contour plot as shown for this situation. What is the new average temperature and temperature at the center of the square?

40 550 35 500 450 30 400 25 350 Y position 20 300 15 250 10 200 150 5 100 10 30 40 20 X position 40 550 35 500 450 30 400 25 350 Y position 20 300 15 250 10 200 150 5 100 10 30 40 20 X position