In code C, please!

The task is to create second-degree polynomial calculator for the function, its integral and

its derivative. A second-degree polynomial is described by the equation

.

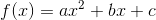Evaluation of the derivative gives the instantaneous slope or rate of change as (where

f' (x) is the derivative of f (x) ):

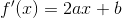
The integral of the function f (x) (let us call it F(x) ) indicates the area underneath the

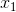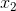curve. Between points and , the area A is

,

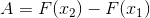where, for a second-degree polynomial,

.

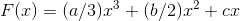Your program will be used to create a table of data of the independent variable x versus

f (x) , f' (x) and A. The user will enter the polynomial coefficients {a,b,c} as well as the

starting value of x (denote it 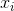), the final value of x (denote it 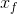), and the increment

value between successive x values (denote it 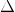x ).

Follow these detailed instructions:

1. First, read this document in its entirety. After reading this handout, you may

optionally create a design sheet for the problem. Your design sheet should help you

determine what header files, functions and variables you will need as well as

identifying expected test results. You do NOT turn in your design sheet.

2. When you write your code, include the usual (detailed) comment block including

program name, author, date, inputs, outputs and description.

3. Create a function of type void to explain the program to the user with the

description printed to the terminal. Do not forget to call the function from main().

4. Input the data while executing from your main() function. Query the user to enter

the data. You must enter the parameters from the user in the following order: a, b, c

and then 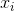, 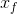and 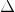x . Use double for all variables and calculations.

5. Your program is to loop over all possible x values in your main() function. The

first x value is to be 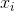, the second 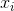+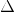x, etc. with the last value being 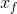(or

somewhat less than 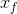if 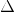x does not divide evenly into the range).

6. The calculation of the area A depends on the initial value of x, 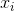. That is, for each x,

we calculate the area as 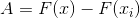. In order to calculate A, you must know

both x and 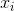. For the first value of x, it should be that A is zero.

7. From main() and for each x, you are to call a function that accepts a, b, c, x and .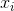

Calculate and return (via pointer operations) f (x) , f' (x) and A. That is, you must

create a single function that accepts eight inputs five are call-by-value (a, b, c, x and

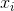), and three are call-by-reference (pointers related to f (x) , f' (x) and A). There

must not be any scan/print statements in your function.

8. Your function uses the values of a, b and c along with the value of x to compute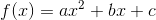

. Similarly, the derivative is computed as 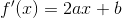. Then,

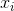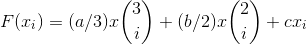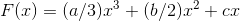using in addition to the other parameters, compute and . The area is found as .

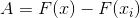Return the result of your calculations back to the main() function (it will be necessary to reference your

outputs via pointers).

9. All output for your table of x versus f (x) , f' (x) and A must be displayed via

statements in your main() function. Write your table to the terminal (i.e., the default

output for printf()). Choose a suitable format for your output numbers.

10. An example of what the output table should look like is given below. Assume that the

user enters 2.0 -2.0 -1.0 for a, b, c, respectively, and 0.0 5.0 0.25 for ,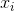

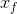and 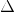x , respectively. Your output should be the following:

f(x) = 2x^2 + -2x + -1

x f(x) f'(x) A

-------------------------------

0.000 -1.000 -2.000 0.000

0.250 -1.375 -1.000 -0.302

0.500 -1.500 0.000 -0.667

0.750 -1.375 1.000 -1.031

1.000 -1.000 2.000 -1.333

1.250 -0.375 3.000 -1.510

1.500 0.500 4.000 -1.500

1.750 1.625 5.000 -1.240

2.000 3.000 6.000 -0.667

2.250 4.625 7.000 0.281

2.500 6.500 8.000 1.667

2.750 8.625 9.000 3.552

3.000 11.000 10.000 6.000

3.250 13.625 11.000 9.073

3.500 16.500 12.000 12.833

3.750 19.625 13.000 17.344

4.000 23.000 14.000 22.667

4.250 26.625 15.000 28.865

4.500 30.500 16.000 36.000

4.750 34.625 17.000 44.135

5.000 39.000 18.000 53.333

11. Use the test set as given above.

f(1) = ax + bx+c f'(2) = 2ax + b A = F(.22) - F(21) F(x) = (a/3). + (6/2) + cx A = F(I) - FX;) F(3:1) = (a/3)() + (6/2)-(3) + c3 A = F(I) - FX;)