In Example 4.1 we looked at the Cobb-Douglas utility function U(x, y)= x^alpha * y^(1-alpha), where 0

few more attributes of that function.

Show explicitly how the compensation required to offset the effect of an increase in the price of x is related to the size of

the exponent a.

Here is the solution to this problem. I do not understand the last part where

starting from

"As a1

C U* (P'x - Px)

As a0

C U* Py(P'x - Px)

Hence, greater the value of a, smaller is the compensation required"

Could you explain step-by-by what this explanation that is in the above quotation?

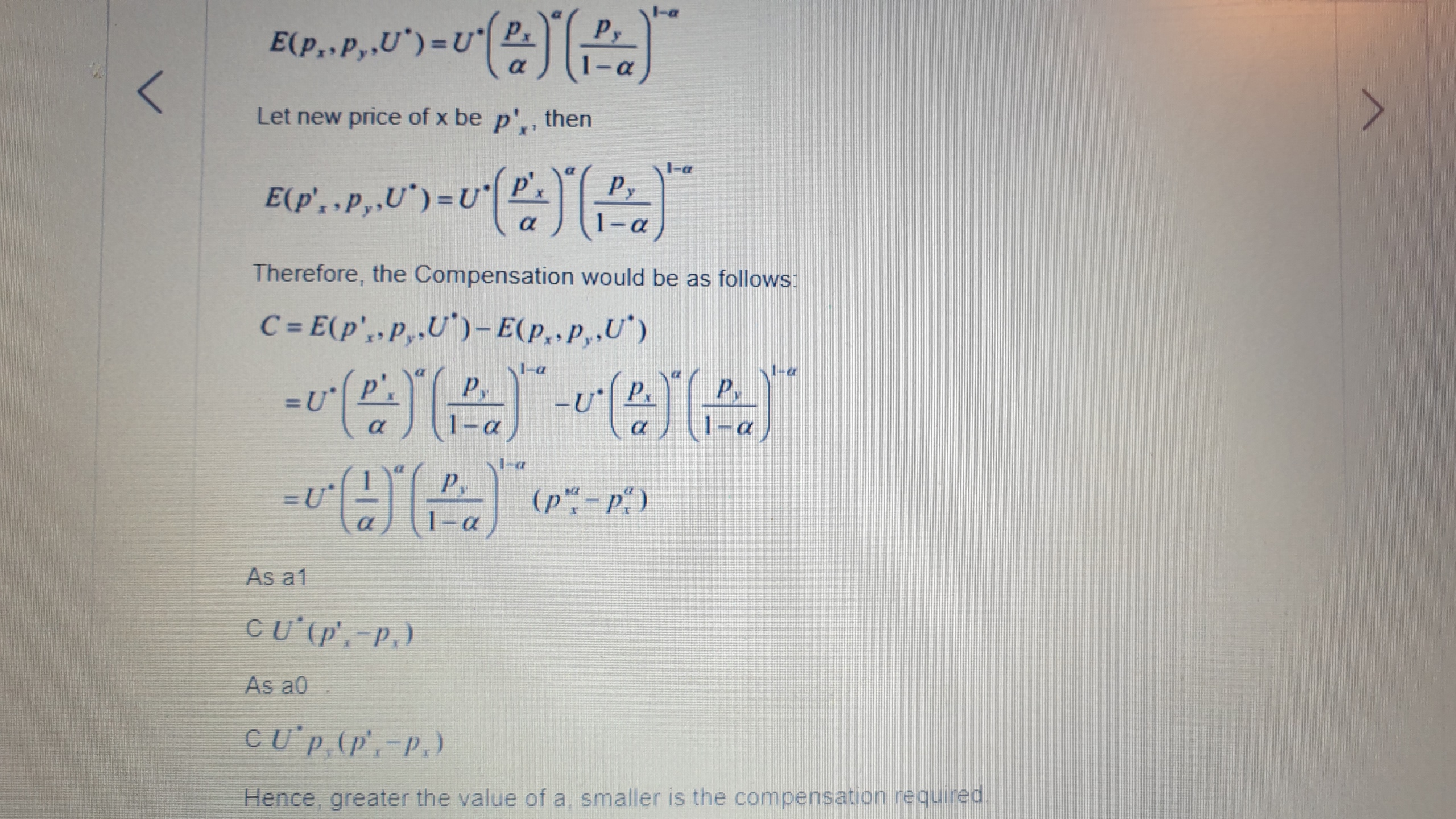
E(P., P, , U.) =UP. P, - a Let new price of x be p', , then Therefore, the Compensation would be as follows C = E(P's, P,. U') - E( P., P,, U' ) As a1 C U'(P' ,=P.) As a0 CU'P, ( P', P.) Hence, greater the value of a, smaller is the compensation required