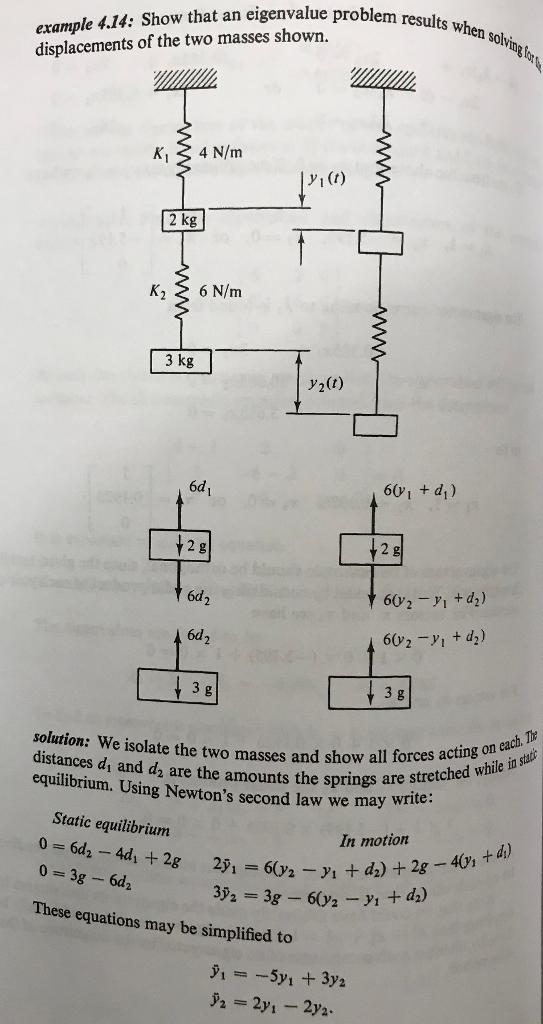
In Example 4.14, without assigning the spring constants and masses any specific values, determine the elements in the coefficient matrix A. Use M = 2, M = 2, K = 12, and K = 8. a) What are the eigenvalues and unit eigenvectors? b) What is the most general solution? c) Find the specific solutions for y(t) and y2(t) if y(0) = 0, y(0) = 0, (0) = 0, and 2(0) = 10. example 4.14: Show that an eigenvalue problem results when solving for displacements of the two masses shown. K K 4 N/m |y(t) 2 kg 6 N/m 3 kg y2(t) www 6d 6(y + d) 2g 2 g 6d2 6d2 6(2y+d) 602-y+d) 3 g 3 distances d, and d are the amounts the springs are stretched while in static solution: We isolate the two masses and show all forces acting on each. The equilibrium. Using Newton's second law we may write: Static equilibrium 0=6d2-4d1+28 0 = 3g - 6d2 In motion 2016(y2y1 + d) +28-4(y,+ d) 32=3g-6(y2-y + d2) These equations may be simplified to 91-5y1+3y2 2 = 2y1-2y2-