In $($Figure $1),$ a

$=0\mathrm{.}9$ in$.$

Figure$1$ of $1$

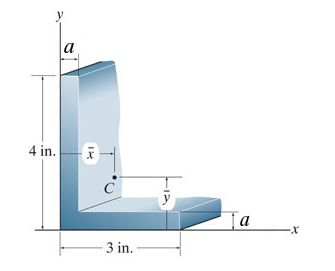
An L shaped cross section of a beam composed of two parts is shown in the x y plane. The x axis points horizontally to the right. The y axis points vertically upward. The corner of the cross section is at the origin. The first part is a rectangle with a height of $\text{'}$a$\text{'}$ and a width of $3$ inches with its left and bottom edges on the positive y and x axes, respectively. The second part is a rectangle with a height of $4$ inches and a width of $\text{'}$a$\text{'}.$ Its left edge lies on the positive y axis, and its bottom edge lies on top of the first part. Point C is located in the first quadrant within the cross section inside the corner at point with coordinates x bar, y bar.

Part A

Locate the centroid x$$

of the cross$-$sectional area.

Express your answer to three significant figures and include the appropriate units.

Activate to select the appropriates template from the following choices. Operate up and down arrow for selection and press enter to choose the input value typeActivate to select the appropriates symbol from the following choices. Operate up and down arrow for selection and press enter to choose the input value type

x$$

$=$

nothing

nothing

Request Answer

Part B

Locate the centroid y$$

of the cross$-$sectional area.

Express your answer to three significant figures and include the appropriate units.

Activate to select the appropriates template from the following choices. Operate up and down arrow for selection and press enter to choose the input value typeActivate to select the appropriates symbol from the following choices. Operate up and down arrow for selection and press enter to choose the input value type

y$$

$=$