In general, for an m n matrix A, the iterative GE procedure continues for K steps until the matrix A^(K) is the zero matrix or the entries are sufficiently small in magnitude. It can be proved that K is at most min(m, n). We hope that

B = 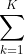A ^(k?1) (:, j_k)A ^(k?1) (i_k , :)/A ^(k?1) (i_k , j_k)

is a good approximation to A with K

clear all;

F = imread(cameraman.tif); % read the figure;

F is matrix figure, imshow(F); % plot the figure

A = dct2(F); % discrete cosine transform;

idct2(A) will recover F; % we apply GE to A;

K = 30; % the maximum steps

n = size(A);

I_row = 1:n(1);

I_col = 1:n(2);

B = zeros(n); % B stores the approximation to A;

% Once B is obtained; plot the compressed figure by

FF = idct2(B);

FF = uint8(FF);

figure, imshow(FF);

(a) Complete the above Matlab code and generate the compressed figures with K = 30, K = 50, K = 100, K = 200.

Hint: You can use the following code to locate the pivot:

M, m] = max(abs(A(:)));

[i_row, i_col]= ind2sub(size(A),m);

and then

A = A - A(I_row,i_col)*A(i_row,I_col)/A(i_row,i_col);

I was given this image compression problem in Matlab. I know

you cannot eliminate A and then add to B. The order should be

B = B + A(I_row,i_col)*A(i_row,I_col)/A(i_row,i_col);

A = A - A(I_row,i_col)*A(i_row,I_col)/A(i_row,i_col);

However I am not sure where to go from there if someone can show me how to do it for K = 30 I am sure I can do the others.

k=1 k=1