IN java

This project builds on the Recursion Exercises lab for this week. In the same project workspace that you downloaded for the lab, you will find three other methods to write. For each of these methods you will need to consider a recursive algorithm.

The first method involves implementing Euclid's Greatest Common Divisor algorithm. The greatest common divisor of two numbers is the largest number that evenly divides them both. For example, the greatest common divisor of 28 and 32 is 4, because 4 is the largest number that divides 28 (7*4) and 32 (8*4). The greatest common divisor of 49 and 28 is 7, because 7 is the largest number that divides 49 (7*7) and 28 (7*4). If two numbers have no other common divisors, the greatest common divisor is 1 - for example the GCD of 7 and 9 is 1 because there are no other divisors.

Euclid's algorithm is as follows - for two numbers m and n where m >= n and both m and n are greater than 0:

• If n evenly divides m with no remainder leftover, then gcd(m,n) is n.
• Otherwise, gcd(m,n) = gcd( n, m % n)

Let's see some examples:

Consider 32 and 28 - gcd(32,28) should be 4 (as discussed above).

• gcd(32, 28) - 28 doesn't evenly divide 32, so gcd(32,28) = gcd(28, 4).
• gcd(28, 4) - 4 evenly divides 28, so gcd(32, 28) is 4.

Consider 49 and 28 - gcd(49,28) should be 7.

• gcd(49, 28) - 28 doesn't evenly divide 49, so gcd(49,28) = gcd(28, 21)
• gcd(28,21) - 21 doesn't evenly divide 28, so gcd(28,21) = gcd(21, 7)
• gcd(21, 7) - 7 evenly divides 21, so gcd(21,7) is 7

The contract for this method is:

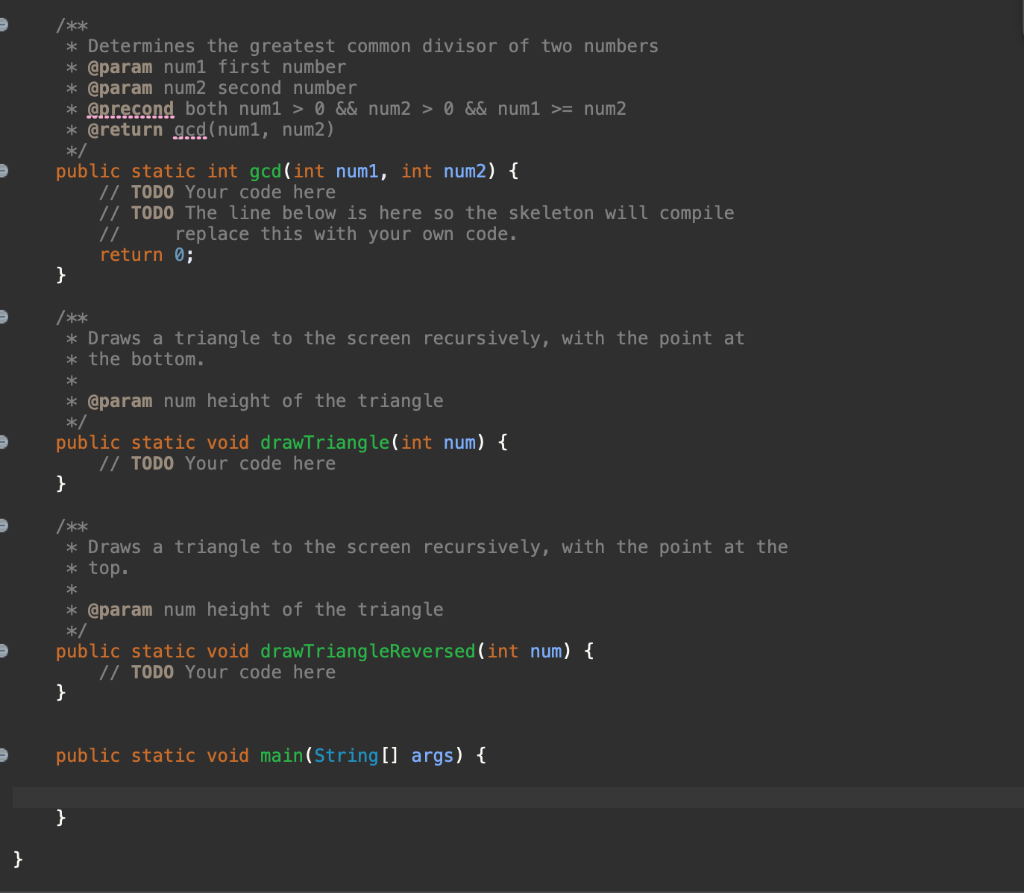
/** * Determines the greatest common divisor of two numbers * @param num1 first number * @param num2 second number * @precond both num1 > 0 && num2 > 0 && num1 >= num2 * @return gcd(num1, num2) */ public static int gcd(int num1, int num2)

Use the algorithm defined above to write this method based on the contract. You can use the main method as a "scratch" area to test your implementation, and there are a series of JUnit tests in the tests folder that you should use to see if your code is working.

The second method has the following contract:

/** * Draws a triangle to the screen recursively, with the point at * the bottom. * * @param num height of the triangle */ public static void drawTriangle(int num)

For this method if the parameter passed is less than or equal to zero it should print nothing. Otherwise it should print a triangle based on the value of the parameter passed:

drawTriangle(1) * drawTriangle(2) ** * drawTriangle(3) *** ** * drawTriangle(4) **** *** ** *

Notice the recursive nature of the triangle - each larger triangle contains it's next smallest triangle within it. A triangle of size 4 is a line of length 4 with a triangle of size 3 below it. A triangle of size 3 is a line of length 3 with a triangle of size 2 below it and so on. Even a triangle of size 1 is a line of length 1 with a triangle of size 0 below it (remember that for size 0 we print nothing).

Develop a recursive algorithm for this behavior, then code it as the drawTriangle method. Use the main method as scratch space to develop your code, and there are JUnit test cases to run against your code when you are finished. (If your main method looks correct but the JUnit test cases are failing, it's possible you are printing an extra blank line somewhere - make sure that for a triangle of size 0 you print nothing not even an empty line!)

The third method has a slightly different contract:

/** * Draws a triangle to the screen recursively, with the point at the * top. * * @param num height of the triangle */ public static void drawTriangleReversed(int num)

This method is exactly as the above, except the triangle should have its point at the top of the screen. Again a triangle of size 0 or less should print nothing, but for positive value it will look something like this:

drawTriangle(1) * drawTriangle(2) * ** drawTriangle(3) * ** *** drawTriangle(4) * ** *** ****

Again, keep the recursion in mind for this - a triangle of size 4 is a triangle of size 3 with a line of length 4 under it. The main method can be used to debug your code, and there are JUnit test cases available to make sure your code is correct.

/*** * Determines the greatest common divisor of two numbers * @param num1 first number * @param num2 second number * @precond both num1 > 0 && num2 > 0 && num1 >= num2 * @return god (numi, num2) */ public static int gcd(int numi, int num2) { // TODO Your code here // TODO The line below is here so the skeleton will compile replace this with your own code. return 0; } /** * Draws a triangle to the screen recursively, with the point at * the bottom. * @param num height of the triangle */ public static void drawTriangle(int num) { // TODO Your code here } * /** * Draws a triangle to the screen recursively, with the point at the * top. * @param num height of the triangle */ public static void drawTriangleReversed (int num) { // TODO Your code here } public static void main(String[] args) { } }