Question: Given a graph G, a matching in G is a set M of edges such that no vertex of G is incident to two

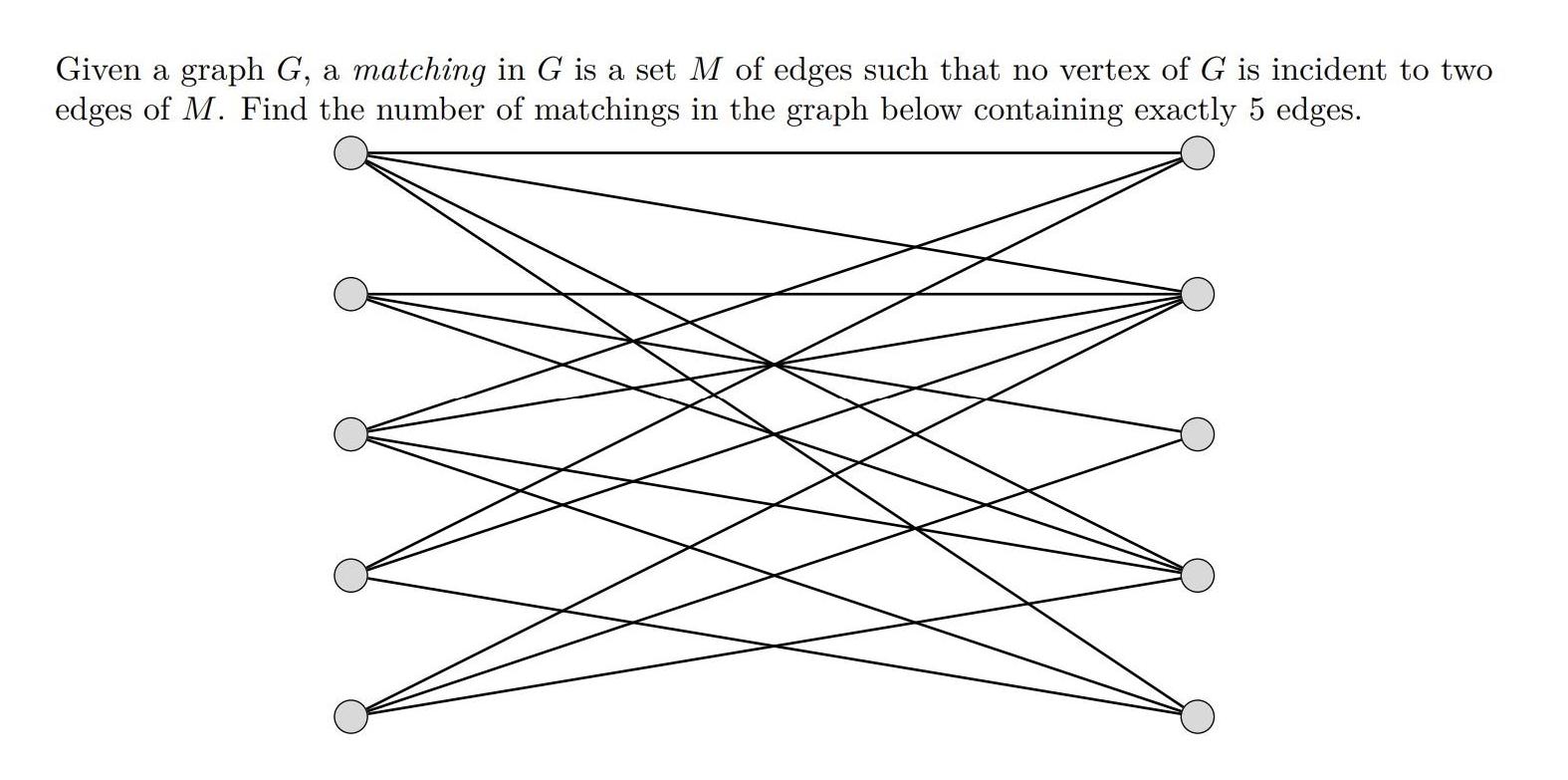
Given a graph G, a matching in G is a set M of edges such that no vertex of G is incident to two edges of M.

Given a graph G, a matching in G is a set M of edges such that no vertex of G is incident to two edges of M. Find the number of matchings in the graph below containing exactly 5 edges. Given a graph G, a matching in G is a set M of edges such that no vertex of G is incident to two edges of M. Find the number of matchings in the graph below containing exactly 5 edges. Given a graph G, a matching in G is a set M of edges such that no vertex of G is incident to two edges of M. Find the number of matchings in the graph below containing exactly 5 edges.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Step 11 To find the number of matchings in the graph containing exactly 5 edges we can use the conce... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

It is estimated that the day Mt. St. Helens erupted (May 18, 1980), about 4.0 105 tons of SO2 were released into the atmosphere. If all the SO2 were eventually converted to sulfuric acid, how many...

It is estimated that while world coffee prices hover around 50 per pound, production costs are around 80 per pound. According to a report issued in September 2002 by the relief agency Oxfam, prices...

It is estimated that 90 billion plastic carry-out bags are produced annually in the United States. In recent years, the number of tons of plastic bags that are recycled has grown exponentially from...

Because export taxes on food commodities are frequently seen as falling on foreign consumers, they tend to be favored as revenue sources by many countries. What assumptions are necessary for export...

Logan, Ltd. makes two products, tables and chairs, which must be processed through assembly and finishing departments. Each table requires 5 hours to assemble and 3 hours to finish, but each chair...

1. Do you agree with Facebooks philosophy of automatically enrolling users in new features without their knowledge or consent? Why or why not? 2. What concerns might a Facebook user have with the Tag...

For the random variable X, it is known that E(X4) = 50, E(2X2 + 7) = 17. Then the variance of the variable Y = X2 equals (a) 25 (b) 50 (c) 75 (d) 94 (e) 100

A plant asset with a cost of $40,000 and accumulated depreciation of $36,000 is sold for $6,000. Required a. What is the book value of the asset at the time of sale? b. What is the amount of gain or...

There is no condition under which a principal must indemnify an agent for a tort claim arising from the agency relationship. Group of answer choices True False

You are reviewing audit work papers containing a narrative description of the Tenney Corporations factory payroll sys-tem. A portion of the narrative is as follows: Factory employees punch time clock...

The authorised capital of a limited company is BD. 5 , 000,000 divided into 5 0,000 equity shares of BD.100 each. Out of these, some shares have been issued to the public, payable BD. 25 on...

As the Financial Director, you have been evaluating annual operating costs as you put together the budget for the next fiscal year. You've noticed that waste metal recycling costs increased last year...

A component for a rocket launch mechanism has a reliability of 80%. For safety, the launch reliability must be greater than 99.9%. How many of the components must be placed in parallel to achieve...

Obje For Exercises 39-40, determine whether the intermediate value theorem guarantees that the function has a zero on the given interval. (See Example 5) - 39. f(x)=2x-7x14x + 30 a. [1, 2] c. [3,4]...

A rocket thrust chamber contains a propellant of molecular weight M = 25 and a specific heat ratio of ? = 1.2. The chamber pressure is pc = pt = 10 MPa, and the combustion temperature is Tc = Tt =...

Give at least 5 possible survey questions for research study entitled "The level of customer satisfaction towards self ordering kiosk on selected fast food chains" that are answerable by "satisfied,...

(couldnt fit full image here so i will type full question) Portage Bay Enterprises has no debt, $0.7 million in cash, and is expected to have free cash flow of $15 million next year. It is then...

Use the information given about the angles and to find the exact value of: (a) sin( + ) (b) cos( + ) (c) sin( - ) (d) tan ( + ) (e) sin(2) (f) cos (2) (g) sin /2 (h) cos/2 cos = 4/5, 0 Answered: 1 week ago

The Plant Department of the local telephone company purchased four special pole hole diggers 8 years ago for $14,000 each. They have been in constant use to the present. Owing to an increased...

If your interest rate is 8%, what is the expected value of the present worth of the "extra" insurance payments in Problem 10-9. In Problem 10-9 You recently had an auto accident that was your fault....

A city is in need of increasing its rubbish disposal facilities. There is a choice of two rubbish disposal areas, as follows. Area A: A gravel pit with a capacity of 16 million cubic meters. Owing to...

An amusement park has opened a new roller coaster. It is so popular that people are waiting for up to 3 hours for a 2-minute ride. Concerned about how patrons (who paid a large amount to enter the...

Consider each of these situations. Do you think the proposed sampling method is appropriate? Explain. a) We want to know what percentage of local doctors accepts Medicaid patients. We call the...

Dairy inspectors visit farms unannounced and take samples of the milk to test for contamination. If the milk is found to contain dirt, antibiotics, or other foreign matter, the milk will be destroyed...