In PYTHON 3

Would like an alternative approach to this question. See answer below the question.

def morph(S, B): ''' Input: - S: a list of distinct Vecs - B: a list of linearly independent Vecs all in Span S Output: a list of pairs of vectors to inject and eject (see problem description) Example: >>> # This is how our morph works. Yours may yield different results. >>> # Note: Make a copy of S to modify instead of modifying S itself. >>> from vecutil import list2vec >>> from vec import Vec >>> S = [list2vec(v) for v in [[1,0,0],[0,1,0],[0,0,1]]] >>> B = [list2vec(v) for v in [[1,1,0],[0,1,1],[1,0,1]]] >>> D = {0, 1, 2} >>> morph(S, B) == [(Vec(D,{0: 1, 1: 1, 2: 0}), Vec(D,{0: 1, 1: 0, 2: 0})), (Vec(D,{0: 0, 1: 1, 2: 1}), Vec(D,{0: 0, 1: 1, 2: 0})), (Vec(D,{0: 1, 1: 0, 2: 1}), Vec(D,{0: 0, 1: 0, 2: 1}))] True >>> S == [list2vec(v) for v in [[1,0,0],[0,1,0],[0,0,1]]] True >>> B == [list2vec(v) for v in [[1,1,0],[0,1,1],[1,0,1]]] True >>> from GF2 import one >>> D = {0, 1, 2, 3, 4, 5, 6, 7} >>> S = [Vec(D,{1: one, 2: one, 3: one, 4: one}), Vec(D,{1: one, 3: one}), Vec(D,{0: one, 1: one, 3: one, 5: one, 6: one}), Vec(D,{3: one, 4: one}), Vec(D,{3: one, 5: one, 6: one})] >>> B = [Vec(D,{2: one, 4: one}), Vec(D,{0: one, 1: one, 2: one, 3: one, 4: one, 5: one, 6: one}), Vec(D,{0: one, 1: one, 2: one, 5: one, 6: one})] >>> sol = morph(S, B) >>> sol == [(B[0],S[0]), (B[1],S[2]), (B[2],S[3])] or sol == [(B[0],S[1]), (B[1],S[2]), (B[2],S[3])] True >>> # Should work the same regardless of order of S >>> from random import random >>> sol = morph(sorted(S, key=lambda x:random()), B) >>> sol == [(B[0],S[0]), (B[1],S[2]), (B[2],S[3])] or sol == [(B[0],S[1]), (B[1],S[2]), (B[2],S[3])] True ''' result = list() A = set() for z in B: result.append((z,exchange(S,A,z))) S.remove(exchange(S,A,z)) S.append(z) return result

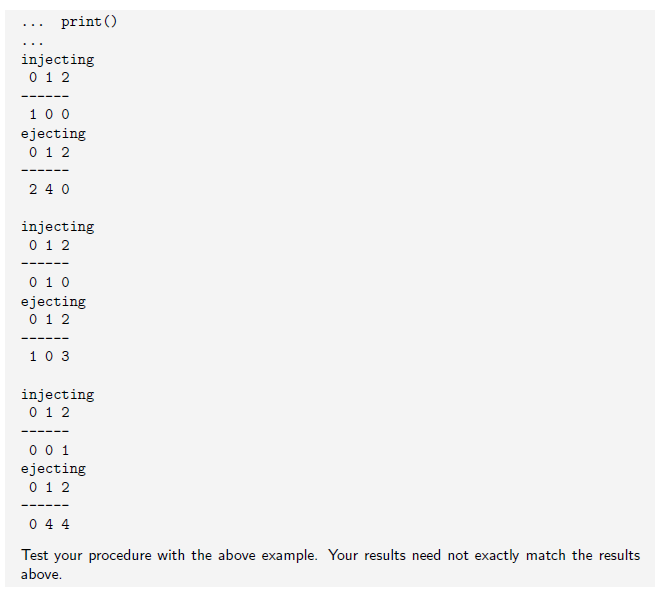
Problem 6.7.4: In this problem, you will write a procedure to achieve the following goal input: a list S of vectors, and a list B of linearly independent vectors such that Span S = output: a list T of vectors that includes B and possibly some vectors of S such that ITI = ISI, and Span T Span S This is not useful in its own sake, and indeed there is a trivial implementation in which T is defined to consist of the vectors in B together with enough vectors of S to make TS. The point of writing this procedure is to illustrate your understanding of the proof of the Morphing Lemma. The procedure should therefore mimic that proof: T should be obtained step by step from S by, in each iteration, injecting a vector of B and ejecting a vector of S - B using the Exchange Lemma. The procedure must return the list of pairs (injected vector, ejected vector) used in morphing S into T. The procedure is to be called morph(S, B). The spec is as follows input: a list S of distinct vectors, and a list B of linearly independent vectors such that output: a k-element list [ , tu! ), (z2, v2), . . . , (zk, tv.) of pairs of vectors such that, for . Span S = Span (S U {,22: . . , 2i)-(U1, u2. . . . , ur,)) where k B! This procedure uses a loop. You can use the procedure exchange(S, A, z) from Prob- lem 5.14.19 or the procedure vec2rep (veclist, u) from Problem 5.14.14 or the solver module Here is an illustration of how the procedure is used >>> S >>> B = [list2vec (v) [list2vec (v) for v for v in in [[2,4,0], [1,0,3], [0,4,4], [1,1,1]]] [[1,0,0], [0,1,0], [0,0,1]]] for (z,) in morph (S, B): print("injecting ", z) print ("ejecting ", v)