in python:

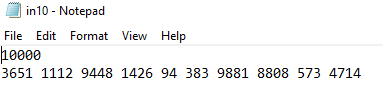
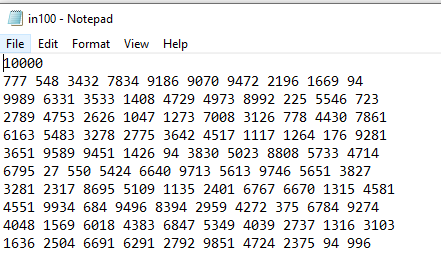
Algorithm Assume that you have n integer numbers that >= 1 and = 1 and

Algorithm Assume that you have n integer numbers that >= 1 and k. You need to sort them in O(n) complexity. Hint use an array of size k, initialize the array elements to zero. Let's name array as A. use numbers from the list as array indexes. When you read a number, simply add 1 to the array element at the appropriate index. Pseudocode for the algorithm will be For number in list A[number] = A[numberl + 1; End For By the end of this loop, the list will be sorted, and all repetitions will be also counted. Now you just need to have another loop to print results from A. For index in range l..k If A[index] is not zero, then output the index as many times as the value of Alindex] End For The time complexity of this algorithm can be estimated as follows Array A initialization is O(k) Storing input numbers in array A is O(n) Printing results checking all array elements is O(k), non-zero elements output is O(n). So, the total complexity is O(k+n). Assuming that k is a constant, the complexity is O(n). What if k is not a constant? In such a case, we will have to use some kind of dynamic storage instead of the array, for example, a vector. The vector is usually implemented as an array that has some spare capacity. When the array is filled, a new array of larger size is created, and all data of the old array is copied to the new array. The new array size is usually two times the old array size. The vector will grow in size as needed, but it means that the vector's elements will be periodically copied that is time consuming. Can you estimate the time complexity as function of k and n?