(IN PYTHON) Use the method of divided differences to find the degree 4 interpolating polynomial P4(x) for the data (0.6,1.433329),(0.7,1.632316),(0.8,1.896481),(0.9,2.247908), and (1.0,2.718282). (b) Calculate P4(0.82) and P4(0.98). (c) The preceding data come from the function f (x) = ex2 . Use the interpolation error formula to find upper bounds for the error at x = 0.82 and x = 0.98, and compare the bounds with the actual error. (d) Plot the actual interpolation errorP(x)ex2 ontheintervals[0.5,1]and[0,2]. This is my code below. Please help me use Matplotlib to solve question D and I have made the graph below for a reference of what it should be when using mat plot lib thank you

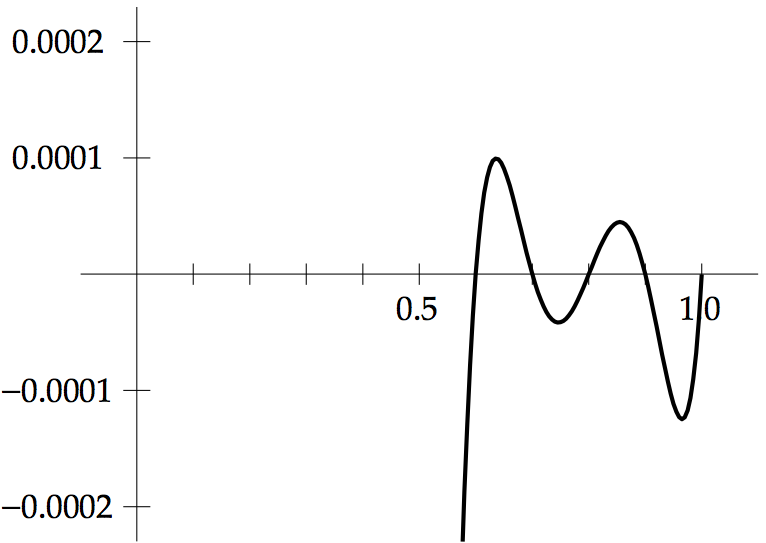
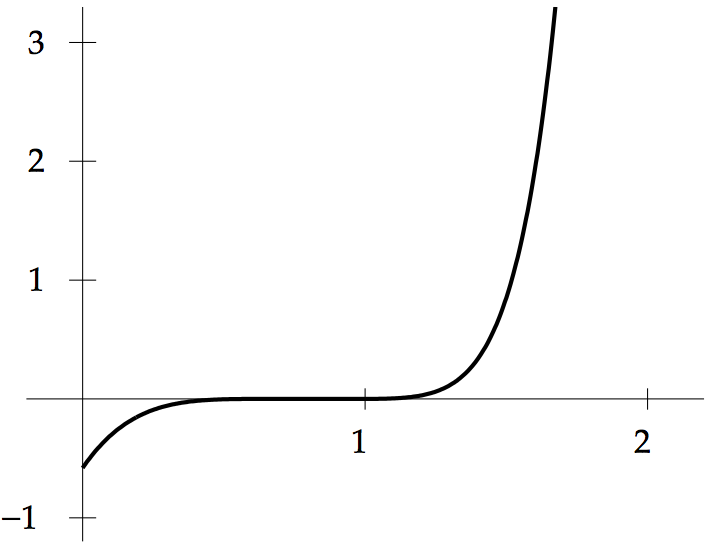
import numpy as np

import matplotlib.pyplot as plt

import math

def divided_diff(x, y):

n = len(x)

coef = [y[0]]

for j in range(1, n):

f = [(y[i]-y[i-1])/(x[i]-x[i-j]) for i in range(j, n)]

y[j:n] = f

coef.append(y[j])

return coef

# Part (a)

x = [0.6, 0.7, 0.8, 0.9, 1.0]

y = [1.433329, 1.632316, 1.896481, 2.247908, 2.718282]

coefficients = divided_diff(x, y)

print("Coefficients:", coefficients)

# Part (b)

def newton_poly(coefficients, x_data, x):

n = len(x_data) - 1

p = coefficients[n]

for k in range(1, n+1):

p = coefficients[n-k] + (x - x_data[n-k])*p

return p

x_1 = 0.82

x_2 = 0.98

P_4_1 = newton_poly(coefficients, x, x_1)

P_4_2 = newton_poly(coefficients, x, x_2)

print(f"P4({x_1}) = {P_4_1:.6f}")

print(f"P4({x_2}) = {P_4_2:.6f}")

# Part (c)

def f(x):

return math.exp(x**2)

def error_bound(x, x_data, f):

n = len(x_data)

max_deriv = 312 * math.exp(1)

prod = 1

for i in range(n):

prod *= abs(x - x_data[i])

return (max_deriv * prod) / math.factorial(n)

e_1 = math.sqrt((f(x_1) - newton_poly(coefficients, x, x_1))**2)

e_2 = math.sqrt((f(x_2) - newton_poly(coefficients, x, x_2))**2)

bound_1 = error_bound(x_1, x, f)

bound_2 = error_bound(x_2, x, f)

print(f"|e({x_1})^2 - P4({x_1})|

print(f"|e({x_2})^2 - P4({x_2})|

print(f"The actual errors, using the results of part (b), are")

print(f"|e({x_1})| {e_1:.7f}")

print(f"|e({x_2})| {e_2:.7f}")