In Python, what is the best way to code for a 2D array and check the nearest neighbors within the array using Von Neumann neighborhood? For example: creating a 2D array of a bunch of zeros (acts as a map) and a single zero in the array changes to a 1 (infected). Then you check for the nearest neighbors from the newly changed 1 but instead of checking all of the '1's neighbors, you only check for the neighbors that are directly above, below, left, and right of the 1.

The code below is what I have for creating the array and checking the nearest neighbors that include the corner but how do I code for only checking for the neighbors that are directly above, below, left, and right of the 1

Thank you in advance!

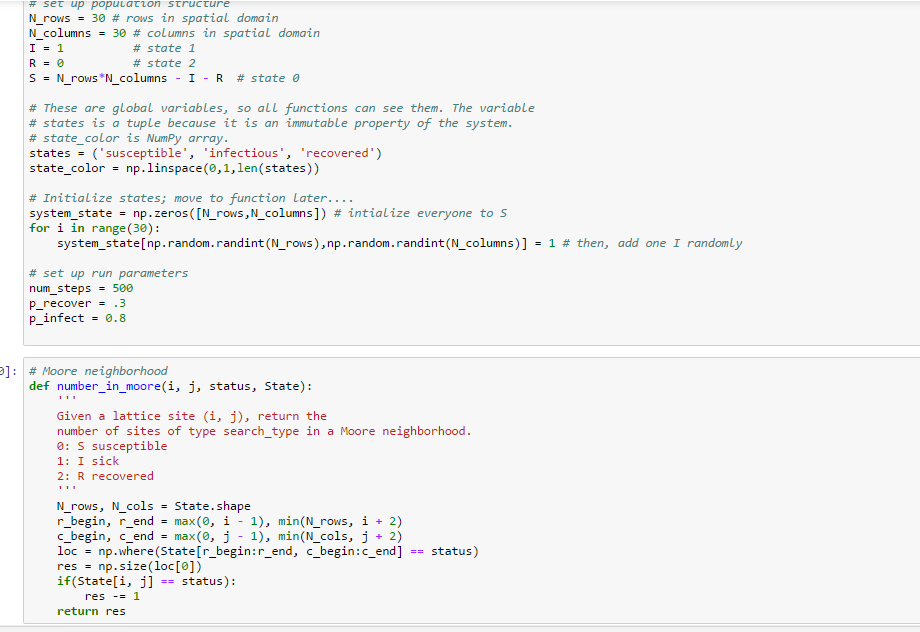
set up popu ation structure N rows 3 30 rows in spatial domain N columns 30 columns in spatial domain state 1 state 2 rows N columns state 0 These are global variables. so all functions can see them. The variable states is a tuple because it is an immutable property of the system. state color is NumPy array. states susceptible infectious recovered state color np li states)) nspace Initialize states move to function Later.... system state np. Zeros ([N rows, N columns intialize everyone to S for i in range (30) system state np. random andint (N andint (N columns 1 then add one I randomly set up run parameters num steps 500 recover p p infect 0.8 0]: Moore neighborhood def number in e Cl j, status, State) moor Given a lattice site (i, j), return the number of sites of type search type in a Moore neighborhood. 0: S susceptible 1: I sick 2: R recovered N rows, N cols 3 State shape r begin, r end 3 max (0 i 1) min (N rows, i 2) begin c end max (0, j 1) min(N cols, j 2) loc np. here (state[r begin: r end, c begin c end] status res 3 np. size(l [0]) OC if(Stateli, j] status) res return res set up popu ation structure N rows 3 30 rows in spatial domain N columns 30 columns in spatial domain state 1 state 2 rows N columns state 0 These are global variables. so all functions can see them. The variable states is a tuple because it is an immutable property of the system. state color is NumPy array. states susceptible infectious recovered state color np li states)) nspace Initialize states move to function Later.... system state np. Zeros ([N rows, N columns intialize everyone to S for i in range (30) system state np. random andint (N andint (N columns 1 then add one I randomly set up run parameters num steps 500 recover p p infect 0.8 0]: Moore neighborhood def number in e Cl j, status, State) moor Given a lattice site (i, j), return the number of sites of type search type in a Moore neighborhood. 0: S susceptible 1: I sick 2: R recovered N rows, N cols 3 State shape r begin, r end 3 max (0 i 1) min (N rows, i 2) begin c end max (0, j 1) min(N cols, j 2) loc np. here (state[r begin: r end, c begin c end] status res 3 np. size(l [0]) OC if(Stateli, j] status) res return res