Question: In robotics, a scheme, known as the Minimum Distance Technique (MDT) is used to avoid line obstacles. The MDT involves the calculation of the minimum

In robotics, a scheme, known as the Minimum Distance Technique (MDT) is used to avoid line obstacles. The MDT involves the calculation of the minimum distance from the robot to the line segment and the avoidance of the resultant point on the line segment. Avoidance of the closest point on the line at any time t is greater than equal to zero, essentially results in the avoidance of the entire line segment. Consider the Figure 3. Show that

(a, -a,) (b, -4) i=(x-a,)e+(y-b)d where e= and d (a, -a,) +(b,

1. Determine the parametric equations of the line.

2. Find the Euclidean distance from the robot to the line segment.

3. Optimize the distance.

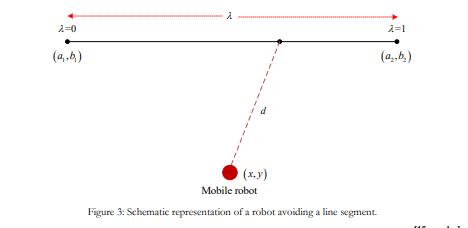
-h) (a, -a,) +(b, -b)

(a, -a,) (b, -4) i=(x-a,)e+(y-b)d where e= and d (a, -a,) +(b, -h) (a, -a,) +(b, -b)

Step by Step Solution

★★★★★

3.44 Rating (173 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Absorption of Drugs The concentration of a drug in an organ at any time t (in seconds) is given by S0.3t - 18(1 - e-t/60) 18e-t/60 - 12e-(t - 20)/60 if t > 20 if 0 sts 20 C(t) where C(t) is measured...

At any time t seconds the distance x meters of a particle moving in a straight line from a fixed point is given by: x=4t + ln(1-t). Determine (a) the initial velocity and acceleration, (b) the...

Avoidance is a risk-control technique that can be used effectively in a risk management program. a. What is the major advantage of using the technique of avoidance in a risk management program? b. Is...

A curve, called a witch of Maria Agnesi, consists of all possible positions of the point P in the figure. Show that parametric equations for this curve can be written as x = 2a cot θ y = 2a...

A string is wound around a circle and then unwound while being held taut. The curve traced by the point P at the end of the string is called the involutes of the circle. If the circle has radius and...

A string is wound around a circle and then unwound while being held taut. The curve traced by the point P at the end of the string is called the involute of the circle. If the circle has radius and...

On March 1, the project manager received three status reports indicating resource utilization to date. Shown below are the three reports as well as the PERT diagram. a. As of the end of week 4, how...

A financial advisor at Diehl Investments identified two companies that are likely candidates for a takeover in the near future. Eastern Cable is a leading manufacturer of flexible cable systems used...

For the problem specified in the table, build upon the results of the original problem to determine the minimum factor of safety for fatigue at point A, based on infinite life. If the life is not...

Menus are attached to windows by calling method____________. A) addMenuBar B) setJMenuBar C) setMenu D) addJMenuBar 67. The first argument to method showMessageDialog specifies A) the title B) the...

What types of companies have: a.a high PE ratio and a low market-to-book ratio? b.a high PE ratio and a high market-to-book ratio? c.a low PE ratio and a high market-to-book ratio? d.a low PE ratio...

A payeoli clerk accidentally entered an employee's hours worked for the week as 3 9 0 instead of 3 a . The data entry conerol that would best prevent this error would be A limit check A check digit....

The following information is from the materials requisitions and time tickets for Job 9-1005 completed by Great Bay Boats. The requisitions are identified by code numbers starting with the letter Q...

The following information is from the materials requisitions and time tickets for Job 9-1005 completed by Franklin Boats. The requisitions are identified by code numbers starting with the letter Q...

You have approached your local bank for a start-up loan commitment for $250,000 needed to open a computer repair store. You have requested that the term of the loan be one year. Your bank has offered...

Logan B. Taylor is a widower whose wife, Sara, died on June 6, 2011. He lives at 4680 Dogwood Lane, Springfield, MO 65801. He is employed as a paralegal by a local law firm. During 2013, he had the...

Logan B. Taylor is a widower whose wife, Sara, died on June 6, 2013. He lives at 4680 Dogwood Lane, Springfield, MO 65801. He is employed as a paralegal by a local law firm. For 2015, he reported the...

Imagine that you are a project auditor reviewing the staging of the world cup. What objectives do you think might be difficult to measure?

In 2 0 2 0 , Tot Toys Inc. purchased a toy manufacturer in Hong Kong, HK Robotics, for $ 1 5 billion. HK Robotics was well known in the industry for producing robotic canine companions. After the...

c In robotics a scheme known as the Minimum Distance Technique MDT is used to avoid line obstacles The MDT involves the calculation of the minimum distance from the robot to the line segment and the...

Damian Williams, the United States Attorney for the Southern District of New York, announced today that JUAN TACURI, a senior promoter in the cryptocurrency Ponzi scheme known as Forcount (and later...

Recall the heat equation which we solved numerically T= = DTxx There we implemented an explicit numerical scheme (FTCS) which led to a conditionally stable solution - meaning that for certain time...

ue for hiding a secret message within a larger document or picture in such a way that others cannot contents of the hidden message is called discern the presence or The earliest known, and simplest...