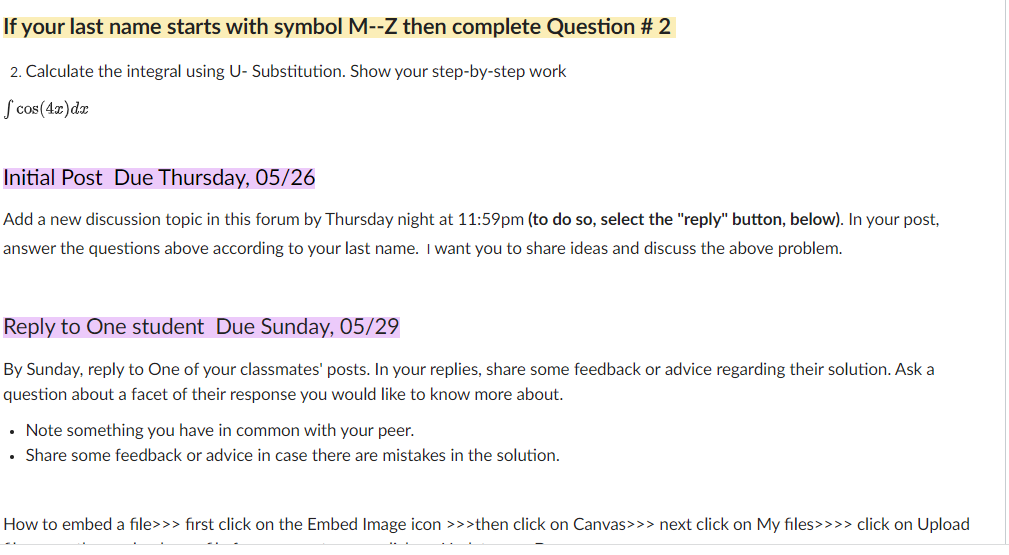
In section 5.5, I discussed using the substitution rule to integrate functions that do not have elementary antiderivatives. For example, If we were given the following integral and we wanted to find the antiderivative , then this is how to use u-substitution: eva dx you can see that the integrand f (x) = eve does not have an elementary antiderivative, and also we can not simplify the expression. Thus we have to use u-sub. Since the exponential function e" is composed with the v@ , then we suggest that u = Va>>>>u=x? >>> du = 1x"?da >> > 2du = a"?da >>> > 2du = da Now plug everything back into the given integral to convert it into a simpler integral that is in terms of u da = f _. eva . dx = fevi . . dx = 2 fe"du = 2e" >>> > F (x) = 2eva + C Here is your assignment If your last name starts with symbol A--L then complete Question # 1 1. Calculate the integral using U- Substitution. Show your step-by-step work /cosx. V1 + sinx. dxIf your last name starts with symbol M--Z then complete Question # 2 2. Calculate the integral using U- Substitution. Show your step-by-step work I oos(4z)d:c Initial Post Due Thursday, 05/26 Add a new discussion topic in this forum by Thursday night at 11:59pm [to do so, select the "reply" button, below}. In your post. answer the questions above according to your last name. I want you to share ideas and discuss the above problem. Reply to One student Due Sunday, 05f29 By Sunday. reply to One of your classmates' posts. In your replies, share some feedback or advice regarding their solution. Ask a question about a facet of their response you would like to know more about. - Note something you have in common with your peer. - Share some feedback or advice in case there are mistakes in the solution. How to embed a le>>> rst click on the Embed Image icon >>>then click on Canvas>>> next click on My les>>>> click on Upload