Question: In the previous Problem Set question, we started looking at the cost function C ( ), the cost of a firm producing & items. An

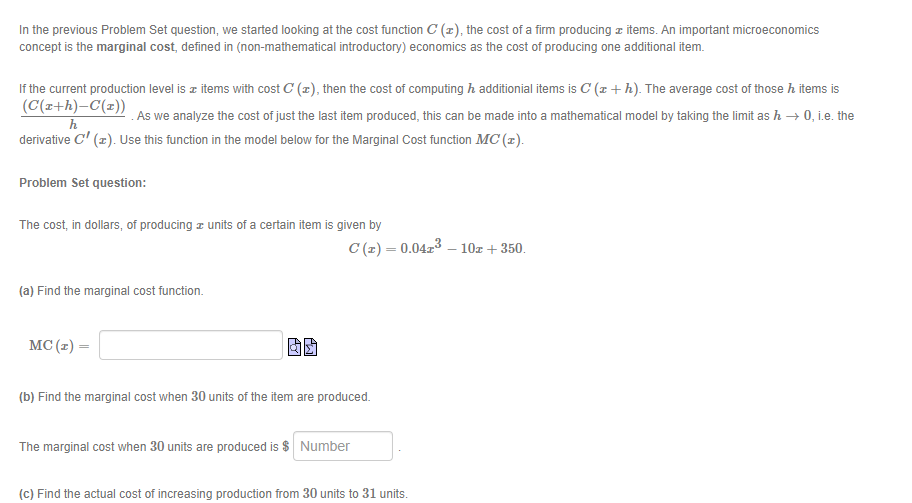
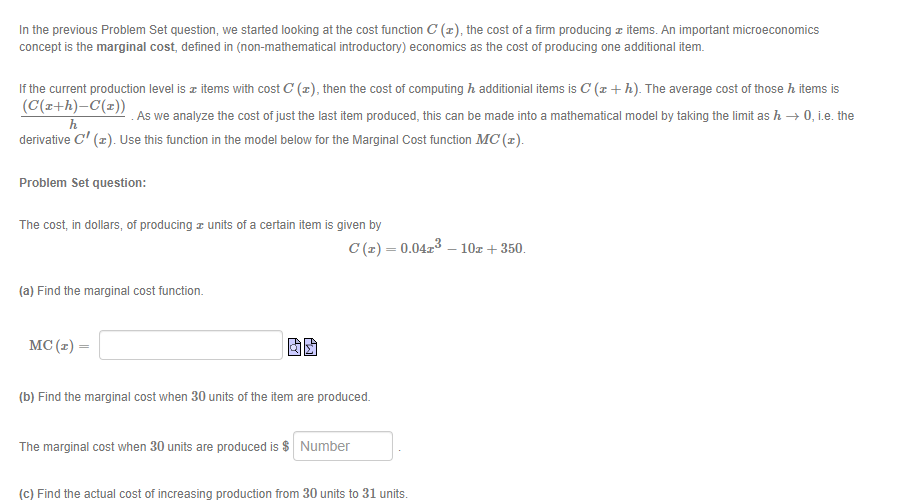
In the previous Problem Set question, we started looking at the cost function C ( ), the cost of a firm producing & items. An important microeconomics concept is the marginal cost, defined in (non-mathematical introductory) economics as the cost of producing one additional item. If the current production level is a items with cost C (x), then the cost of computing h additionial items is C (x + h). The average cost of those h items is (C(Ith)-C(I)) h As we analyze the cost of just the last item produced, this can be made into a mathematical model by taking the limit as h -+ 0, i.e. the derivative C(x). Use this function in the model below for the Marginal Cost function MC (I). Problem Set question: The cost, in dollars, of producing z units of a certain item is given by C(x) = 0.04r3 - 10r + 350. (a) Find the marginal cost function. MC(I) = (b) Find the marginal cost when 30 units of the item are produced. The marginal cost when 30 units are produced is $ Number (c) Find the actual cost of increasing production from 30 units to 31 units

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

everything is write except the MC question a). The part with the arrow Introduction to Calculus in Economics (continued): In the previous Problem Set question, we started looking at the cost function...

Introduction to Calculus in Economics (continued): In the previous Problem Set question, we started looking at the cost function C (x), the cost of a firm producing z items. An important...

In the previous Problem Set question, we started looking at the cost function C ( ), the cost of a firm producing a items. An important microeconomics concept is the marginal cost, defined in...

6 Introduction to Calculus in Economics (continued): In the previous Problem Set question, we started looking at the cost function C (m), the cost of a firm producing w items. An important...

please help Introduction to Calculus in Economics (continued): In the previous Problem Set question, we started looking at the cost function C(), the cost of a firm producing z items, An important...

please help 20 Southern New Hampshire University - estion 6: (6 points) Introduction to Calculus in Economics (continued): In the previous Problem Set question, we started looking at the cost...

Introduction to Calculus in Economics (continued): In the previous Problem Set question, we started looking at the cost function C (11:), the cost of a firm producing m items. An important...

Please help solve and explain Introduction to Calculus in Economics (continued): In the previous Problem Set question, we started looking at the cost function C (x), the cost of a firm producing w...

Introduction to Calculus in Economics (continued): In the previous Problem Set question, we started looking at the cost function C (z), the cost of a firm producing z items. An important...

Introduction to Calculus in Economics (continued): In the previous Problem Set question, we started looking at the cost function C (:I). the cost of a firm producing I items. An important...

Jack and Jill need to save $7000 toward a new car. How long will it take them if they save $200 a month earning interest at 4.2% per year? ( Treat as an ordinary annuity.) (State your answer in years...

Governmental auditing can extend beyond audits of financial statements to include audits of an agencys efficient and economical use of resources and a. Constitutionality of laws and regulations...

BE16.4 (LO 1) Carow SA purchased on January 1, 2025, as a held-for-collection investment, 60,000 of the 8%, 5-year bonds of Harrison, Inc. for 65,118, which provides a 6% return. The bonds pay...

Yellow Press, Inc., buys paper in 1 , 5 0 0 - pound rolls for printing. Annual demand is 2 comma 2 5 0 2 , 2 5 0 rolls. The cost per roll is $ 1 comma 0 0 0 1 , 0 0 0 , and the annual holding cost is...

Inventory Valuation Turnbell Manufacturing held no inventory at the beginning of March. Inventory purchases by the company during March were as follows: Turnbell uses a periodic inventory system. At...

Perpetual Inventory Methods Clifton Enterprises uses a perpetual inventory system under which inventory costs and cost of goods sold are recomputed after each inventory transaction. During March, the...

Inventory Turnover Field Company reported total inventory at January 1 and December 31, 2000, of $200,000 and $160,000, respectively. Cost of goods sold for 2000 was $470,000. Fields nearest...