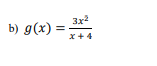
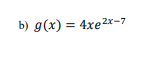
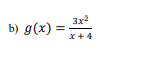
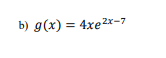
In the work for problems 1 (a-b), 2, and 3 (a-b} it is expected that you will clearly show ALL of the following: 1) The number lines representing the appropriate derivative{s) for the problem. 2) Any test values that you are using. 3) Either the lll calculations andfor sign charts that you are using to establish the signs of the derivatives. Simply recording what the signs on the number line are without supporting work is NOT enough and voids any answers given to the problem regardless of whether they are correct or not. While using a graphing calculator to CHECK your solutions for these problems is perfectly acceptable, the whole point of this course is to use calculus and not the graphing capabilities of a calculator to solve problems and if the calculus supporting work is not shown you will lose most {if not all} of the points for the problem. If you are unsure what my expectations are for what needs to be shown, look at the work that I show for the rst two examples in the 13.11132 lecture {you should be showing basically a_ll of the work that I am showing in those examples). 1) For each of the following: (i) Determine the intervals on which the following functions are increasing and decreasing. (ii) Use the first derivative test to classify each of the critical points as a relative minimum, a relative maximum, or neither one. Make sure that you read the directions on the front cover before attempting problems 1, 2, and 3 and I STRONGLY recommend that you review the lecture examples referenced in those instructions to lessen the possibility of losing points due to not showing the necessary work to support your answers. a) f(x) = x*+ 12x3 - 72x3 + 216\f2) Suppose that the total profit P(x) (in dollars) to manufacture a quantity x of pumpkin spice soda (in thousands of gallons) is given by the function P(x) = -x + 39x -144x -1313. {12 pts) a) What is a reasonable domain for this function? b) Determine the interval(s) on which P(x) is increasing and the interval(s) on which P(x) is decreasing.3) For each of the following, determine the intervals on which the following functions are concave up and concave down. a) f (x) = =x*+ 4x3 -63x2 + 124x\f4) Suppose that a homeowner wishes to construct a Halloween petting zoo in his backyard consisting of an enclosure of four parallel rectangular pens that are fenced on all four sides as shown: Rose Hair Vampire Ghost Tasmanian Tarantulas Bats Crabs Devils If he has a total of 2600 feet of fencing available to use to construct the enclosure, what is the maximum TOTAL area that can be enclosed?5) Suppose that a company decides to raise capital by selling stock. Over the next 10 years the average monthly price of the stock fluctuates according to the rule S(t) = 0.21 5 - 1.89t + 40.90 where S(t) is in dollars per share and r is the number of months since the stock was first offered for sale (this means that S(t) is only valid on the interval [0. 120]). Determine the maximum and minimum prices of the stock (in dollars and cents) and when these prices occurred.6) After / hours on a particular day on the railways of the Island of Sodor, Toby the tram engine is s(t) = -0.203 + 1.902 + 11.1t miles east of Knapford Station (for 0 s t $ 12). a) Where is Toby (both distance and direction from the starting point at Knapford Station) after 5 hours? b) What is the velocity of Toby after 5 hours? c) What is the acceleration of Toby after 5 hours? d) Is Toby speeding up or slowing down after 5 hours? How can you tell?7) Find the absolute extreme values of f(x) = x* + 12x3 - 104x on the interval [-4, 5 ]. 8) A star fruit grower finds that if she plants 21 trees per acre, each tree will yield 90 bushels of star fruit. She also estimates that for each additional tree that she plants per acre, the yield of each tree will decrease by 2 bushels. How many trees should she plant per acre to maximize her harvest and what is the maximum harvest