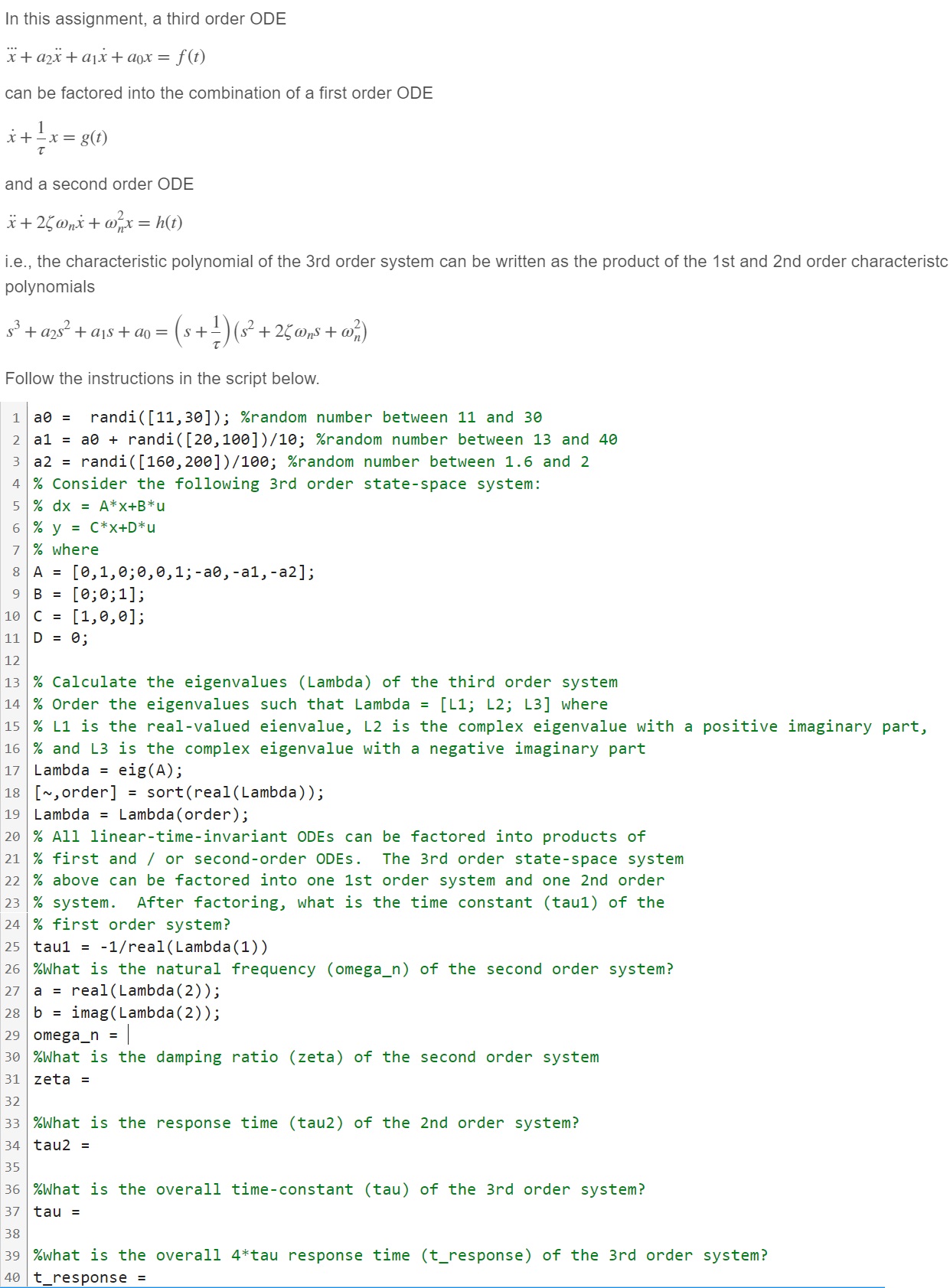
In this assignment, a third order ODE

$x^{}+a_2{x}^{}+a_1{x}^{}+a_{0}x=f(t)$

can be factored into the combination of a first order ODE

$x^{}+\frac{1}{}x=g(t)$

and a second order ODE

$x^{}+2{}_n{x}^{}+{}_n^{2}x=h(t)$

i$.$e$.,$ the characteristic polynomial of the $3$ rd order system can be written as the product of the $1$ st and $2$ nd order characteristc

polynomials

$s^3+a_2{s}^2+a_{1}s+a_0=(s+\frac{1}{})(s^2+2{}_{n}s+{}_n^2)$

Follow the instructions in the script below.

$a=$randi$([11,30])$;$\%$ random number between $11$ and $30$

$a1=a+$randi$\frac{[20,100]}{10}$;$\%$ random number between $13$ and $40$

$a2=$randi$\frac{[160,200]}{100}$;$\%$ random number between $1\mathrm{.}6$ and $2$

$\%$ Consider the following $3$rd order state$-$space system:

$\%dx=A**x+B**u$

$\%y=C**x+D**u$

$\%$ where

$A=[,1,$;$,,1$;$-a,-a1,-a2]$;

$B=[0$;$$;$1]$;

$C=[1,0,]$;

$D=0$;

$\%$ Calculate the eigenvalues $($Lambda$)$ of the third order system

$\%$ Order the eigenvalues such that Lambda $=[L1$;$L2$;$L3]$ where

$\%$ L$1$ is the real$-$valued eienvalue, L$2$ is the complex eigenvalue with a positive imaginary part,

$\%$ and $L3$ is the complex eigenvalue with a negative imaginary part

Lambda $=$eig$(A)$;

$,$ order