In this assignment, we are going to start working on the parser. The lexer's job is to make "words", the parser's job is to make sure that those tokens are in an order that makes sense and make a data structure in memory that represents the program. The Tokens are in a 1-dimensional structure (array or list). The parser's output will be a 2-dimensional tree.

The parser works using recursive descent. We are encoding the rules into the structure of the program. There are a few simple rules that we will follow in writing our parser:

Each function represents some "phrase" in our language, like "if statement" or "assignment statement".

Each function must either succeed or fail:

On success, remove Tokens from the list and output a tree node

On failure, leave the list unchanged and return null.

When there are alternatives, the function must call each alternative's function until it finds one that is not null.

Details

Nodes

Let's start by building some tree nodes. Each tree node is just a Java class. We will start by defining Node as an abstract class. It should have an abstract ToString() method. Every tree node will extend Node and will end with the word "Node" - IfNode, WhileNode, etc. You should make any constructors for the Nodes that make sense as you go. The ToString() method will be your primary debugging/testing tool, so don't overlook that. The tree will be read-only, so mutators need not be created.

Make two new nodes - IntegerNode and RealNode - extending Node. IntegerNode needs to have an int member. RealNode needs to have a float member. Members should be private, with an accessor. Constructors should take the members as parameters.

Make sure to create a "MathOpNode" (also extending Node) - this represents a math operation. This node should have an enum for the math operations (add, subtract, etc.). It should have two sub-nodes for the left and right sides of the operation. You might thing that these should be IntegerNode or RealNode. But, of course, we have lots of other possibilities. For example, consider that we will need to represent (eventually) x+4. So, our left and right sub-nodes should be of type Node so that we can represent whatever we need.

Parser - setup

Make sure to create a Parser class (does not derive from anything). It must have a constructor that accepts your collection of Tokens. We will be treating the collection of tokens as a queue - taking off the front. It isn't necessary to use a Java Queue, but you may.

We will add three helper functions to parser. These should be private:

matchAndRemove - accepts a token type. Looks at the next token in the collection:

If the passed in token type matches the next token's type, remove that token and return it.

If the passed in token type DOES NOT match the next token's type (or there are no more tokens) return null.

expectEndsOfLine - uses matchAndRemove to match and discard one or more ENDOFLINE tokens. Throw a SyntaxErrorException if no ENDOFLINE was found.

peek - accepts an integer and looks ahead that many tokens and returns that token. Returns null if there aren't enough tokens to fulfill the request.

Parser - parse

Make sure to create a public parse method. There are no parameters, and it returns Node. This will be called from main once lexing is complete. For now, we are going to only parse a subset of Shank V2 - mathematical expressions. Parse should call expression() then expectEndOfLine() in a loop until either returns null. Don't worry about storing the return node but you should print it out (using ToString()) for testing.

The tricky part of mathematical expressions is order of operations. Fortunately, this is fairly easily solved in recursive descent by using a few functions. The intuition is this: accept tokens from the highest priority first. When you can't find any that fit the pattern, fall back to lower priority. The thing that makes this "weird" is that we will call the lowest level first. But it calls the next highest first thing. Let's take a look:

EXPRESSION = TERM { (plus or minus) TERM}

TERM = FACTOR { (times or divide or mod) FACTOR}

FACTOR = {-} number or lparen EXPRESSION rparen

Notice the curly braces - these indicate 0 or more.

expression(), term() and factor() will all be methods of our recursive descent parser. All of them must use matchOrRemove(). The formulae above are very literal. Consider the first one:

EXPRESSION = TERM { (plus or minus) TERM}

expression() calls term(). Then it (in a loop) looks for a + or -. If it finds one, it calls term again and constructs a MathOpNode using the two term() returns as the left and right. That MathOpNode becomes the left if there are more +/- sign. So 1+2+3 becomes:

MathOpNode(+,IntegerNode(1),(MathOpNode(+,IntegerNode(2),IntegerNode(3)))

Let's look at a complete example: 3*-4+5: our tokens will look something like this:

NUMBER TIMES MINUS NUMBER PLUS NUMBER ENDOFLINE- your token types might differ a little

We will call expression(). The first thing it does is look for a term by calling term(). term() calls factor() first thing. factor() will matchAndRemove MINUS and not find it. It then tries NUMBER succeeds.

NUMBER TIMES MINUS NUMBER PLUS NUMBER ENDOFLINE

It looks at the NUMBER node, sees no decimal point and makes an IntegerNode (3) and returns it. term() gets the IntegerNode from factor() and now should loop looking for TIMES or DIVIDE. It finds a TIMES.

NUMBER TIMES MINUS NUMBER PLUS NUMBER ENDOFLINE

It should then call factor(). factor() looks for the MINUS. It finds it. It internally notes that we are now in "negative" mode. It then finds the NUMBER. It sees no decimal point and makes an IntegerNode (-4) and returns it.

NUMBER TIMES MINUS NUMBER PLUS NUMBER ENDOFLINE

term() gets the IntegerNode. It constructs a MathOpNode of type multiply with a left and right side of the two IntegerNodes. It now looks for multiply and divide and doesn't find them. It returns the MathOpNode that it has.

Now expression() has a MathOpNode. It looks for plus or minus and finds plus.

NUMBER TIMES MINUS NUMBER PLUS NUMBER ENDOFLINE

Now expression() calls term() which calls factor() which looks for NUMBER, finds it and constructs an IntegerNode (5).

NUMBER TIMES MINUS NUMBER PLUS NUMBER ENDOFLINE

term() won't find a times or divide, so it returns the IntegerNode. expression() now has a + with a left and a right side, so it creates that MathOpNode. It looks for plus/minus, doesn't find it and returns the + MathOpNode. parse() should print the returned Node (the MathOpNode).

expectEndsOfLine() is called and finds an ENDOFLINE.

NUMBER TIMES MINUS NUMBER PLUS NUMBERENDOFLINE

Assuming that was all that was in the input file, the next call to Expression() will return null and we will exit.

Your output can vary a lot. My only requirement is that it shows unambiguously that the tree was constructed correctly. One example:

MathOpNode(+, MathOpNode(*,IntegerNode(3),IntegerNode(-4)),IntegerNode(5))

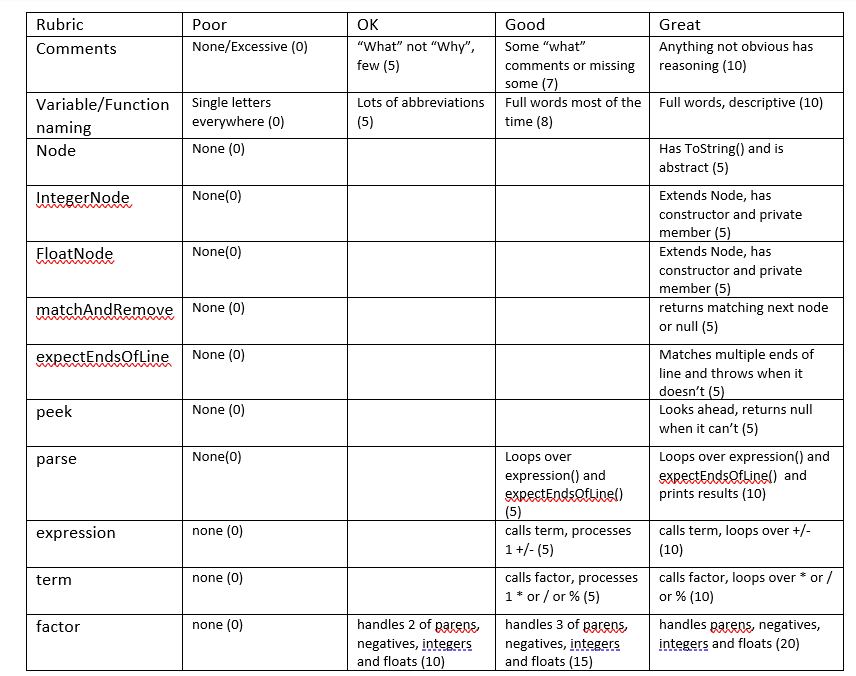
Below is the parser.java. Please fix the errors and make sure the parser.java runs correctly without any error in the code. Attached is the rubric

Parser.java

package mypack;

import java.util.List;

public class Parser { private List tokens; private int currentTokenIndex;

public Parser(List tokens) { this.tokens = tokens; this.currentTokenIndex = 0; }

public Node parse() throws SyntaxErrorException { Node result = null; while (true) { Node expr = expression(); if (expr == null) { break; } expectEndOfLine(); System.out.println(expr.toString()); } return result; }

private Node expression() { Node result = term(); while (true) { Token token = peek(); if (token != null && (token.getType() == TokenType.PLUS || token.getType() == TokenType.MINUS)) { matchAndRemove(token.getType()); Node right = term(); if (right == null) { throw new SyntaxErrorException("Expected right operand after " + token.getValue()); } result = new MathOpNode(token.getType(), result, right); } else { break; } } return result; }

private Node term() { Node result = factor(); while (true) { Token token = peek(); if (token != null && (token.getType() == TokenType.TIMES || token.getType() == TokenType.DIVIDE || token.getType() == TokenType.MOD)) { matchAndRemove(token.getType()); Node right = factor(); if (right == null) { throw new SyntaxErrorException("Expected right operand after " + token.getValue()); } result = new MathOpNode(token.getType(), result, right); } else { break; } } return result; }

private Node factor() { Token token = matchAndRemove(TokenType.MINUS); Node result = null; Token nextToken = peek(); if (nextToken != null) { if (nextToken.getType() == TokenType.NUMBER) { matchAndRemove(TokenType.NUMBER); if (token != null) { result = new IntegerNode(-Integer.parseInt(nextToken.getValue())); } else { result = new IntegerNode(Integer.parseInt(nextToken.getValue())); } } else if (nextToken.getType() == TokenType.IPAR) { matchAndRemove(TokenType.IPAR); result = expression(); matchAndRemove(TokenType.RPAR); } } return result; }

private Token matchAndRemove(TokenType type) { if (peek() != null && peek().getType() == type) { return tokens.get(currentTokenIndex++); } return null; }

private void expectEndOfLine() throws SyntaxErrorException { Token token = matchAndRemove(TokenType.ENDOFLINE); if (token == null) { throw new SyntaxErrorException("Expected end of line"); } }

private Token peek() { return currentTokenIndex