Question: In this exercise, consider a particle moving on a circular path of radius b described by r(t) = b cos(wt)i + b sin(wt)j, where w

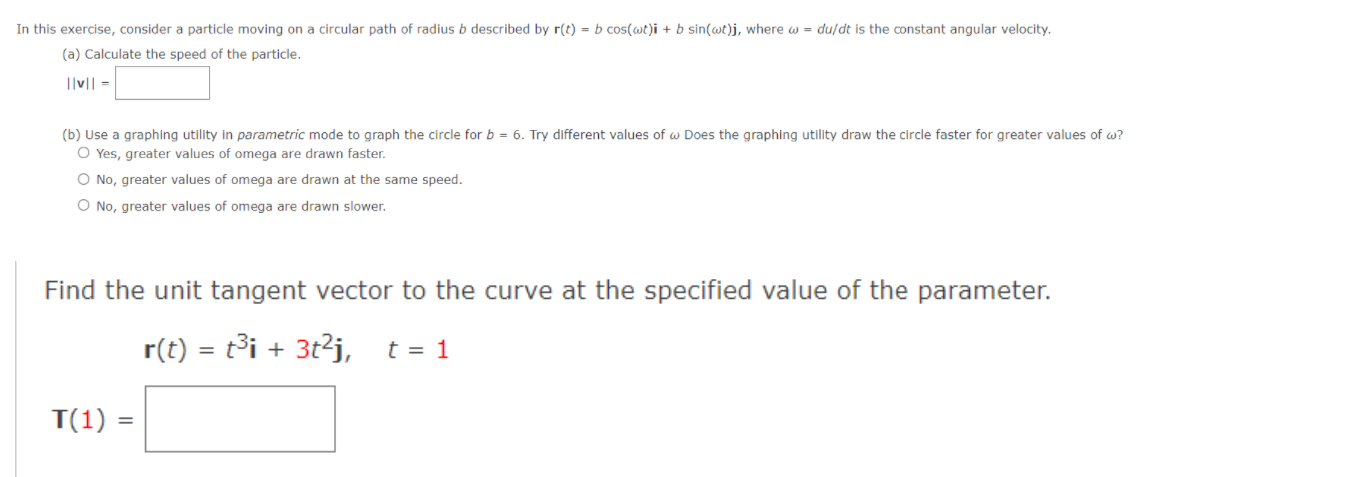
In this exercise, consider a particle moving on a circular path of radius b described by r(t) = b cos(wt)i + b sin(wt)j, where w = du/dt is the constant angular velocity. (a) Calculate the speed of the particle. Itvil = (b) Use a graphing utility In parametric mode to graph the circle for b = 6. Try different values of w Does the graphing utility draw the circle faster for greater values of w? O Yes, greater values of omega are drawn faster. O No, greater values of omega are drawn at the same speed. O No, greater values of omega are drawn slower. Find the unit tangent vector to the curve at the specified value of the parameter. r(t) = +3i + 3taj, t = 1 T(1) =

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

The position vector r describes the path of an object moving in space. Find the velocity v((), speed s(!), and acceleration a(() of the object. r() = 2ti + 9tj + 60k X 11 Oi + 0j + 0kUse the model...

Consider a particle moving on a circular path of radius b described by r(t) = b cos ti + b sin tj, where = du/dt is the constant angular velocity. (a) Show that the speed of the particle is b. (b)...

Consider a particle moving on a circular path of radius b described by r(t) = b cos ti + b sin tj, where = du/dt is the constant angular velocity. Show that the magnitude of the acceleration vector...

Consider a particle moving on a circular path of radius b described by r(t) = b cos ti + b sin tj, where = du/dt is the constant angular velocity. Find the acceleration vector and show that its...

1. [-/1 Points] DETAILS LARCALC11 12.3.004. (a) Find the velocity vector v(f), speed s(f), and acceleration vector a[t) of the object. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER The position vector r...

Consider a particle moving on a circular path of radius b described by r(t) = b cos ti + b sin tj, where = du/dt is the constant angular velocity. Find the velocity vector and show that it is...

E-Physics Tutorial Book Note: I have attached below the lesson for the 3 activities. Thank you so much for your time and effort. Activity 1. Directions: Use the right-hand rule to determine the...

1. 3 2 Consider the function f(x) = x - 3x - 9x + 10, x (a) . Find the equation of the straight line passing through the maximum and minimum points of the graph y = f(x). (4) (b) Show that the point...

ed mr .Er 12. A particle is moving in xy-plane, and its positions are given by F = x(1) ity(1) ; where x(t)=xo cos(wt+ po), y(t)=yo sin(wt+ po) where xo=2 meters, yo=5 meters, =10 s", and do=Tt/3 are...

806 Chapter Fifteen OPTIMIZATION: LOCAL AND GLOBAL EXTREMA If f is not continuous or the region R is not closed and bounded, there is no guarantee that f achieves a global maximum or global minimum...

Estimate the amount of solar energy input to a horizontal collector per year whose surface area is 4 m for Green Bay and Memphis. Determine the equivalent amount of natural gas that would provide the...

The shareholders' equity section of Valade Corp.'s balance sheet is: Required: a. How many shares of common stock were issued during 2010? What was their average issue price? b. How many shares of...

7 Here are three numbered cards. 5 6 7 Sofia puts the cards in a line at random to make a 3-digit number. a List all the possible outcomes. Find the probability that the number is i an odd number iii...

please give me correct answer and there should be no plagiarism in answers 2. How does the buying decision process work in B2B Marketing? 3. What is the specific buying procedure marketers must adapt...

2. In this chapter, the reader should reflect on the following concepts:

1. To provide an understanding of how emotions are regulated by the development of relationships between actors in a communication situation.

Positive effect on trusting others, and also improvements in the final results.