In this problem, we show that the clock's length appears shortened when viewed from a reference frame S in which the clock is moving with relative speed v to the right, parallel to its long axis. The key is to calculate explicitly the length of time that an observer in S will measure between "ticks" of the moving clock in terms of LS , the length of the clock in the S frame. Comparing this with the known period of the clock in the S frame allows us to compute the length of the clock in the S frame. Einstein used gedanken experiments such as this to clarify his thinking as he strove to remove inconsistencies from the basic formulations of physics.

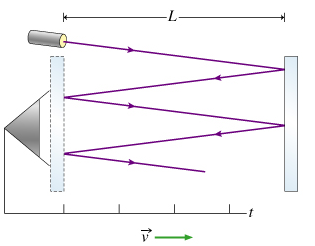
Part A

What is the period t 0 between successive ticks of the clock in its rest frame?

Express your answer in terms of variables given in the introduction. Use c for the speed of light.

t 0 =

2 Lc

SubmitMyAnswersGive Up

Correct

Part B

Use time dilation to determine the time tS between the ticks of the light clock as viewed from reference frame S .

Express the time tS between these ticks in terms of L , the relative speed v , and the speed of light c .

tS =

tS 1? v 2 c 2

SubmitHintsMyAnswersGiveUpReview Part

Incorrect; One attempt remaining; Try Again

We now come to the key step: calculating the round-trip travel time (the clock tick time) from the perspective of an observer in S . This is not trivial, because we know that the separation of the moving mirrors is L in the moving frame, but it is not necessarily L in the stationary reference frame. In fact, the point of this problem is to calculate the length LS of the clock in the system S . We do know that the pulse of light will travel at speed c relative to the coordinate system S . Therefore our job is to find the time tS it takes to catch the moving mirror (which appears to be LS ahead of the detector mirror) and return to the mirror at the end of the clock with the detector mirror.

Part C

What is the round-trip time tS ?

Use kinematics to express tS in terms of LS , the velocity v , and the speed of light c .

tS =	2 LSc (1? v 2 c 2)

SubmitHintsMyAnswersGiveUpReview Part

Correct

Part D

What is the length LS of the clock according to a stationary observer in S ?

Express LS in terms of the length L of the clock in its rest frame and the velocities v and c .

LS =	L (1? v 2 c 2???????)

SubmitHintsMyAnswersGiveUpReview Part

Correct

The length of the moving clock appears shorter to the stationary observer. This is called the Lorentz contraction, but it is a reflection of the fundamental fact that the length of a moving object has lost its conventional meaning in relativity. Length is the spatial separation of two events: The (moving) ends of the clock must be measured at the same instant. Since simultaneity is relative (as a consequence of the relativity postulates), the length of a moving object depends on which observer defines what simultaneous means. Length and time have become relative quantities, as was realized first by Einstein. This property of nature has significant philosophical implications.

Now, click on the image below to launch the video: A Moving Light Clock Appears Shorter. This video shows the situation described in the problem. You can watch the video again at any point.

The video shows the situation you've been studying in motion. The top shows how things look in the rest frame of the clock. On the bottom, you see the same situation from a frame of reference moving relative to the light clock. The clock's motion is set by the value of ? = 1.41 in this case.

Watch the video a few times to be sure that you have a good understanding of how everything works. Note that the rate of the clock in the moving frame is slower than that in the stationary frame.

Part E

Notice that the clocks at the front and rear mirrors of the light clock do not show the same time when viewed from the moving frame. Why is this?

Notice that the clocks at the front and rear mirrors of the light clock do not show the same time when viewed from the moving frame. Why is this?

The front clock experiences a greater time dilation because it moves ahead of the rear clock.

The clocks start simultaneously in the rest frame, so they cannot start simultaneously in the moving frame.

Since the light clock is passing the observer, the signal from the front clock takes longer to reach the observer, making the time appear earlier.

PEARSON 6.67 6.67 7-1.41 6.67 6.67 ALWAYS LEARNING 3.42 8.14 -1.00-101-10/7-709m Brela internet At Mark on 100, 306,