Question: In this problem, y = 1/(x + c) is a one-parameter family of solutions of the first-order DE y' + 2xy2 = 0. Find

y = 1/(x + c) is a one-parameter family of solutions of the first-order DE y' + 2xy2 = 0. Find a solution of

In this problem, y=ce + ce is a two-parameter family of solutions of the second-order DE y

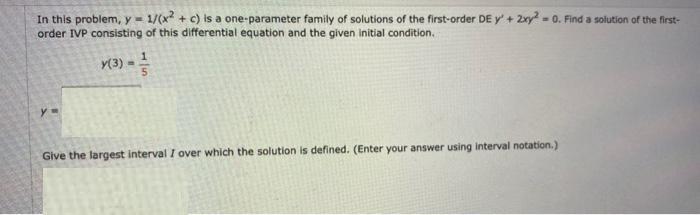
In this problem, y = 1/(x + c) is a one-parameter family of solutions of the first-order DE y' + 2xy2 = 0. Find a solution of the first- order IVP consisting of this differential equation and the given initial condition. y(3) Give the largest interval I over which the solution is defined. (Enter your answer using interval notation.) y = 1/(x + c) is a one-parameter family of solutions of the first-order DE y' + 2xy2 = 0. Find a solution of the first-order IVP consisting of this differential equation and the given initial condition. X(-3) = 1/2 y = Find the domain of y considered as a function over the reals. (Enter your answer using interval notation.) Give the largest interval I over which the solution is defined for the given initial condition. (Enter your answer using interval notation.) In this problem, y=ce + ce is a two-parameter family of solutions of the second-order DE y"-y=0. Find c, and c given the following initial conditions. (Your answers will not contain a variable.) y(1) = 0, y'(1) - e C1 = ON Find a solution of the second-order IVP consisting of this differential equation and the given initial conditions.

Step by Step Solution

★★★★★

3.46 Rating (175 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

In Problem 21 a one-parameter family of solutions of the DE P' = P(1 P) is given. Does any solution curve pass through the point (0, 3)? Through the point (0, 1)? Data from problem 21 Verify that the...

In Example 5 the largest interval I over which the explicit solutions y = 1 (x) and y = 2 (x) are define is the open interval (5, 5). Why cant the interval I of definition be the closed interval 5,...

A one-parameter family of solutions of the first-order differential equation dy/dx = xy 1/2 is y = (1/4 x 4 + c) 2 for c 0. Each solution in this family is dened on (-, ). The last statement is not...

In Exercises verify the particular solution of the differential equation. Solution y = 6x- - 4 sin x + 1. - Differential Equation and Initial Condition y' = 6 - 4 cos x y(0) = 1

In Exercises verify the particular solution of the differential equation. Solution y = e-cos.x Differential Equation and Initial Condition y' = y sin x (7) 2 y = 1

Write an equivalent first-order differential equation and initial condition for y. y = 2- X T 0 (1 + y(t)) sin t dt

Write an equivalent first-order differential equation and initial condition for y. X + * 1 y = -1 + (t - y(t)) dt

You make 2 quarts of salsa for a party. The recipe calls for 5 teaspoons of lime juice per quart, but you had accidentally put in 5 tablespoons per quart. You decide to feed your guests the salsa...

Consider a system represented by a first-order ordinary differential equation: (a) Show first that for a function f(t) using the definition of the derivative. (b) Apply the above result to show that...

In Exercises verify the particular solution of the differential equation. Solution y = 4e-6x Differential Equation and Initial Condition y' = -12xy y(0) = 4

Nelson took her stereo to ABC Stereo for repairs. ABC repaired the stereo at a cost of $150 and informed Nelson that her stereo was ready. Before Nelson came to pick up her stereo, ABC was...

Write down the Limitation of Beer - Lamberts law?

Discuss the Hawthorne experiments in detail

Explain the characteristics of a good system of control

State the importance of control

What are the barriers to effective communication? What measures do you suggest to overcome them?

1st Apr, 2019 Omar invested RO 150,000 in his business. 2nd Apr, 2019 He approached Bank Nizwa to open a bank account to deposited RO 50,000 in it. 1st May, 2019 Omar purchased Construction...

Imagine a sound wave with a frequency of 1.10 kHz propagating with a speed of 330 m/s. Determine the phase difference in radians between any two points on the wave separated by 10.0 cm.

Find the general solution of the given differential equation. Give the largest interval I over which the general solution is defined. Determine whether there are any transient terms in the general...

Solve the given initial-value problem. xy 2 dy/dx = y 3 - x 3 , y(1) = 2

Verify that the indicated function is an explicit solution of the given differential equation. Give an interval of definition I for each solution. 1. y'' + y = 2 cos x 2 sin x; y = x sin x + x cos x...

3. How does Bronfenbrenner describe the different contexts of enculturation?

3.4 Describe how peers contribute to how children learn the values and norms of their culture.

1. Find a cross-cultural study in your library or through any reference source for primary research articles. Try evaluating it using each of the issues raised in this chapter. What differences and...