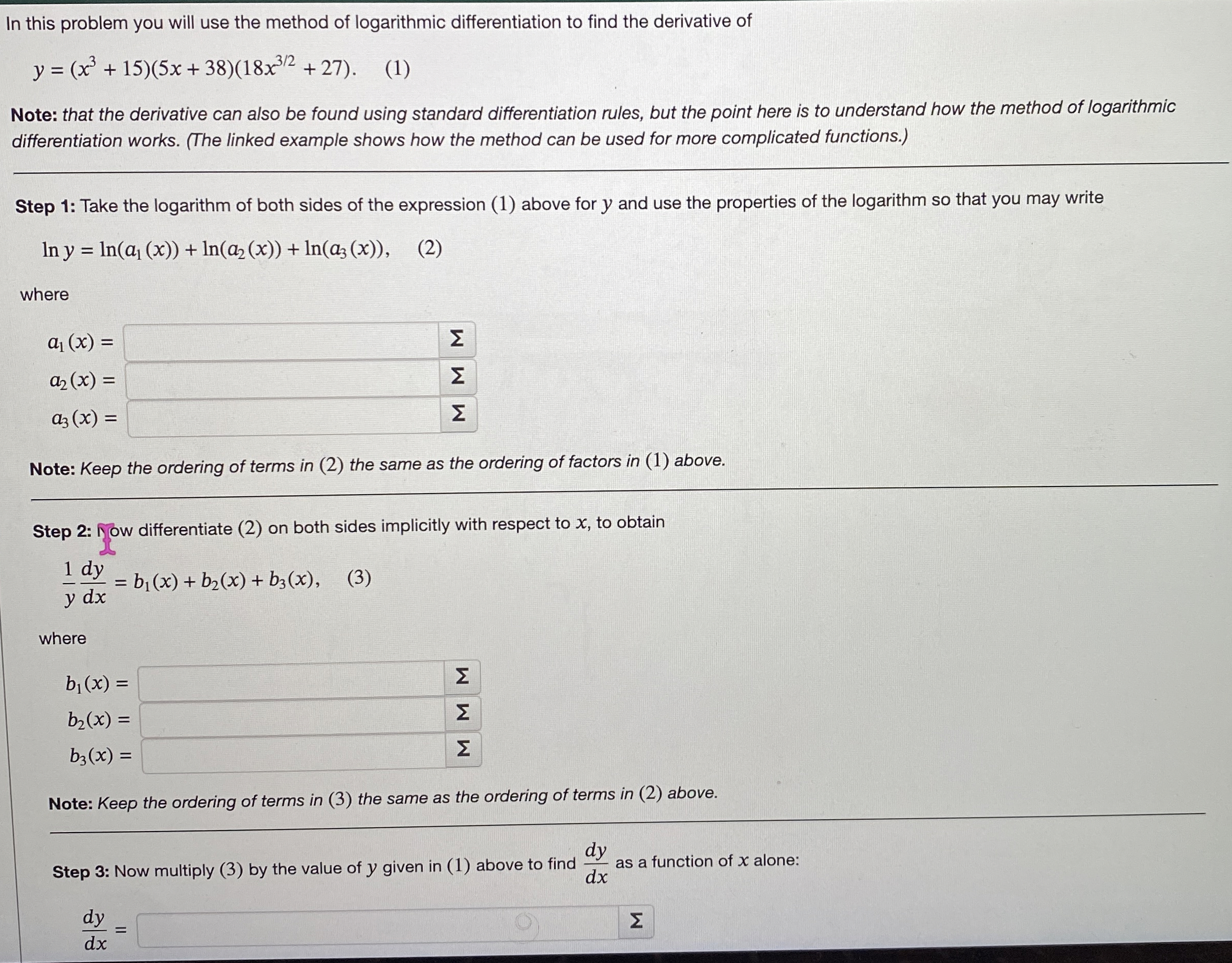
In this problem you will use the method of logarithmic differentiation to find the derivative of

$y=(x^3+15)(5x+38)(18x^{\frac{3}{2}}+27)$

Note: that the derivative can also be found using standard differentiation rules, but the point here is to understand how the method of logarithmic differentiation works. $($The linked example shows how the method can be used for more complicated functions.$)$

Step $1$: Take the logarithm of both sides of the expression $(1)$ above for $y$ and use the properties of the logarithm so that you may write

$lny=ln(a_1(x))+ln(a_2(x))+ln(a_3(x))$

where

$a_1(x)=$

$a_2(x)=$

$a_3(x)=$

Note: Keep the ordering of terms in $(2)$ the same as the ordering of factors in $(1)$ above.

Step $2$: IOw differentiate $(2)$ on both sides implicitly with respect to $x,$ to obtain

$\frac{1}{y}\frac{dy}{dx}=b_1(x)+b_2(x)+b_3(x)$

where

$b_1(x)=$

$b_2(x)=$

$b_3(x)=$

$$

Note: Keep the ordering of terms in $(3)$ the same as the ordering of terms in $(2)$ above.

Step $3$: Now multiply $(3)$ by the value of $y$ given in $(1)$ above to find $\frac{dy}{dx}$ as a function of $x$ alone:

$\frac{dy}{dx}=$

$$