In this project you will construct an increasing function that is discontinuous at each rational point in (0, 1) and continuous at each irrational point in (0, 1). We will need two basic facts:

a. The rational numbers in the interval (0, 1) can be arranged in a sequence {r _n } ^∞ _n=1 . This is true because the set of rational numbers is countable. (See Example 0.12 and Corollary 0.15.)

b. Any rearrangement of an absolutely convergent series converges, and any sub-series of an absolutely convergent series converges. See Theorem 6.16, and apply the comparison test to the subseries, replacing the missing terms with zeros.

For each real number x ∈ (0, 1), define K(x) = {n: r _n ≤ x}. So K(x) is a subset of J, and we define f : (0, 1) → R by the formula

  

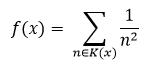
Prove that f is discontinuous at r if r is a rational number.

In this project you will construct an increasing function that is discontinuous at each rational point in (0,1) and continuous at each irrational point in (0,1). We will need two basic facts:

1.) Prove that f is increasing.

2.) Prove that f is discontinuous at r if r is rational.

3.) Prove that f is continuous at x if x is irrational.

Transcribed Image Text:

Σ f(x) = n2 nEK(x) Σ f(x) = n2 nEK(x)

Answer rating: 100% (QA)

Let r 1 n0 0 1 is a rational number and let r 1 11 k1 0 1 is ... View the full answer