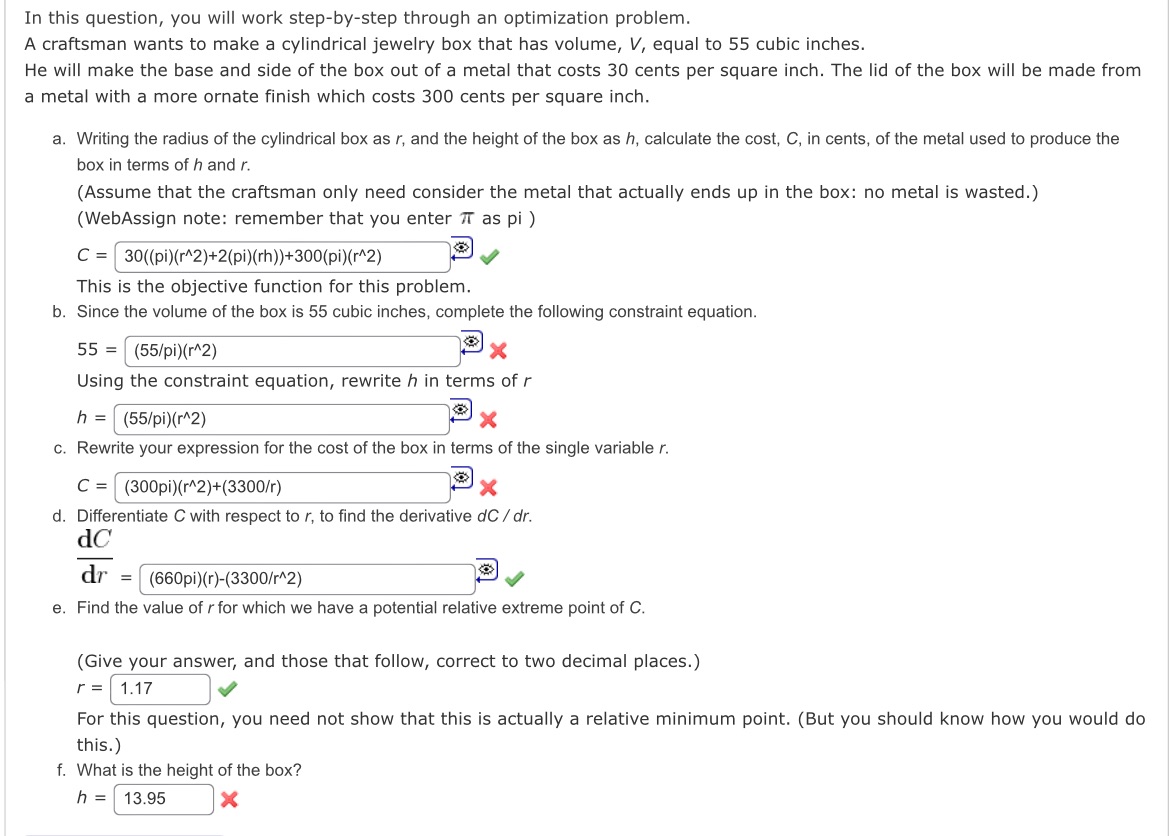
In this question, you will work step-by-step through an optimization problem. A craftsman wants to make a cylindrical jewelry box that has volume, V, equal to 55 cubic inches. He will make the base and side of the box out of a metal that costs 30 cents per square inch. The lid of the box will be made from a metal with a more ornate finish which costs 300 cents per square inch. a. Writing the radius of the cylindrical box as r, and the height of the box as h, calculate the cost, C, in cents, of the metal used to produce the box in terms of h and r. (Assume that the craftsman only need consider the metal that actually ends up in the box: no metal is wasted.) (WebAssign note: remember that you enter as pi ) C=30((pi)^2)+2(pi)(rh))+300(pi)(r^2) This is the objective function for this problem. b. Since the volume of the box is 55 cubic inches, complete the following constraint equation. 55 (55/pi)(2) x Using the constraint equation, rewrite h in terms of r h = (55/pi)(r^2) x c. Rewrite your expression for the cost of the box in terms of the single variable r. C (300pi)(r^2)+(3300/r) d. Differentiate C with respect to r, to find the derivative dC /dr. dC dr (660pi)(r)-(3300/r^2) e. Find the value of r for which we have a potential relative extreme point of C. (Give your answer, and those that follow, correct to two decimal places.) r=1.17 For this question, you need not show that this is actually a relative minimum point. (But you should know how you would do this.) f. What is the height of the box? h = 13.95