Question: In this tutorial, you will use Excel to solve a larger linear program and perform a sensitivity analysis. A company produces three soft toys, an
In this tutorial, you will use Excel to solve a larger linear program and perform a sensitivity analysis.
A company produces three soft toys, an antelope, a bear and a cat. For one day's production run it has available 11 m2 of fur fabric, 24 m2 of wool fabric and 30 glass eyes.
The antelope requires 0.5 m2 of fur fabric, 2 m2 of wool fabric and two eyes. Each sell at a profit of $3. The bear requires 1 m2 of fur fabric, 1.5 m2 of wool fabric and two eyes. Each sell at a profit of $5. The cat requires 1 m2 of fur fabric, 1 m2 of wool fabric and two eyes. Each sell at a profit of $2.
Follow these instructions to solve this linear program and perform a sensitivity analysis.
1. Open the file Excel-Lab-09-Template.xlsx using the desktop version of Microsoft Excel.
2. In A3, type your full name.
3. In C5, type Antelope, in D5 Bear, and in E5 Cat. These are your three variables.
4. In C6:E6, enter a 1. These are placeholder values that will change when we use Solver.
5. In A8, after Objective:, type the objective (maximize or minimize).
6. In C9:E9, enter the coefficients of the objective function.
7. In F9, compute the value of the objective function using references to the coefficients in
C9:E9 and the variable values in C6:E6.
8. In C12:E12, enter the coefficients of the constraint given by fur.
9. In F12, compute the total fur used by referencing the coefficients in C12:D12 and the
variables values in C6:E6.
10. In H12, enter the fur limit.
11. In G12, enter the correct inequality >= or 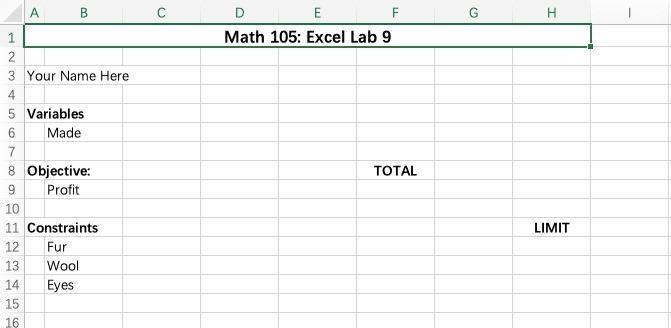
A B F G H E F Math 105: Excel Lab 9 TOTAL 1 2 3 Your Name Here 4 5 Variables 6 Made 7 8 Objective: 9 Profit 10 11 Constraints 12 Fur 13 Wool 14 Eyes 15 16 LIMIT12. Repeat Steps 8 to 11 for constraints given by wool and glass eyes.
13. In the Ribbon, click the Data tab. Open the Solver dialog.
14. Change Set Objective to the value of the objective function.
15. Choose Max or Min, depending on your objective.
16. Set By Changing Variable Cells to the dummy variables you set for Antelope, Bear, and
Cat in C6:E6.
17. Click Add. Add the three constraints by setting the totals in the Cell Reference, selecting
the correct inequality, and setting the constraint value.
18. Ensure that Make Unconstrained Variables Non-Negative and set the Solving Method to
Simplex LP. Click Solve.
19. Solver should present the Solver Results dialog. Click OK. In Report, select Sensitivity.
The solution has now been saved the variable values in C6:D6.
20. Open the Sensitivity Report sheet. Copy the Variable Cells and Constraints tables. Paste
these in the original sheet, in A16 underneath the linear program.
21. Underneath the sensitivity analysis, answer the following questions:
a. How many of each toy should be produced to maximize profit according to these constraints?
b. How many of each toy should be produced to maximize profit, if the profit for Antelope toys was $5 instead of $3? Why?
c. Without rerunning the linear program, can you tell how many of each toy to produce if the Bear toys had a profit of $7? Why or why not?
d. How much would Cat toys have to profit before being worth producing?
e. How much would profit increase if we had 13 m2 of fur to work with?
f. How much would profit decrease if we had only 20 m2 of wool to work with?
g. Without rerunning the linear program, can you tell if profit would change if we
had 26 glass eyes to work with? Why or why not?

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


