In your script, write a function called polar2cart that accepts a polar coordinates of a point as input parameters (radius.in, angle.in), and returns a two-element vector for the point in Cartesian coordinates c(xcoord, ycoord). You may assume the input angle is in radians. Recall the transformation from polar to rectangular/Cartesian coordinates:

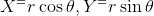
a.) In your script, add code to test the function for (radius =1, theta=0) and (radius=1, theta=pi/6).

b.) Then add the following code to create an annotated plot of a point with radius=1 and theta=pi/4. Edit to include your name and include the plot in your report.

xy.test# transform to x-y coordinates

x1

plot(x1,y1,xlab="x-coord",ylab="y-coord",

main=bquote("Your Name: angle = " ~ pi/4))

# x0, y0 (tail of arrow) followed by x1, y1 (head of arrow)

arrows(0,0,x1,y1,col="red")

# x0, y0, x1, y1 # horizontal segment

segments(0,y1,x1,y1, lty="dashed")

# x0, y0, x1, y1 # vertical segment

segments(x1,0,x1,y1, lty="dashed")

2. Add a function to your script called cart2polar that accepts a Cartesian/rectangular coordinate as input (xcIN, ycIN), and converts it to polar coordinates (radius, angleDeg), where the output angle is in degrees.

Add code to test the function for three sets of input (xcoord,ycoord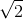) = (1/, 1/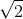), (0,1), and (1,0).

3. A frustum is a mathematical lampshade. Consider the following equation for computing the area of a right circular frustum with major radius R (bottom), minor radius r (top), and height h.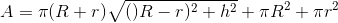

The volume of a right circular frustum is given by the following equation.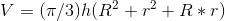

a.) Add a function to your script called calculateFrustProps that returns the surface area and volume as a two-element vector given three inputs (rad.major, rad.minor, and height).

b.) Complete and add the following code to your script to calculate the frustum area and volume for input r=1, R=2, and h=3. For the blanks, your goal is to extract the area and volume as separate variables from myFrustAV.

frust_AV

height=____)

# extract area and volume from vector

area

vol

cat("Frustum Area =", area)

cat("Frustum Volume =", vol)

4. A cone is a special case of the frustum. Think about how the frustum area and volume mathematically reduce to a cone.

a.) Write a function called calculateConeProps that has two inputs (radius and height) and returns the area and volume of a cone by calling your calculateFrustProps function in the body. One input of the frustum function will be fixed and the other two equal to the input of the cone function.

b.) Add and complete the code to test the function with radius=1 and height=5.

cone_AV

cone_area

cone_vol

cat("Cone Area =", cone_area)

cat("Cone Volume =", cone_vol)