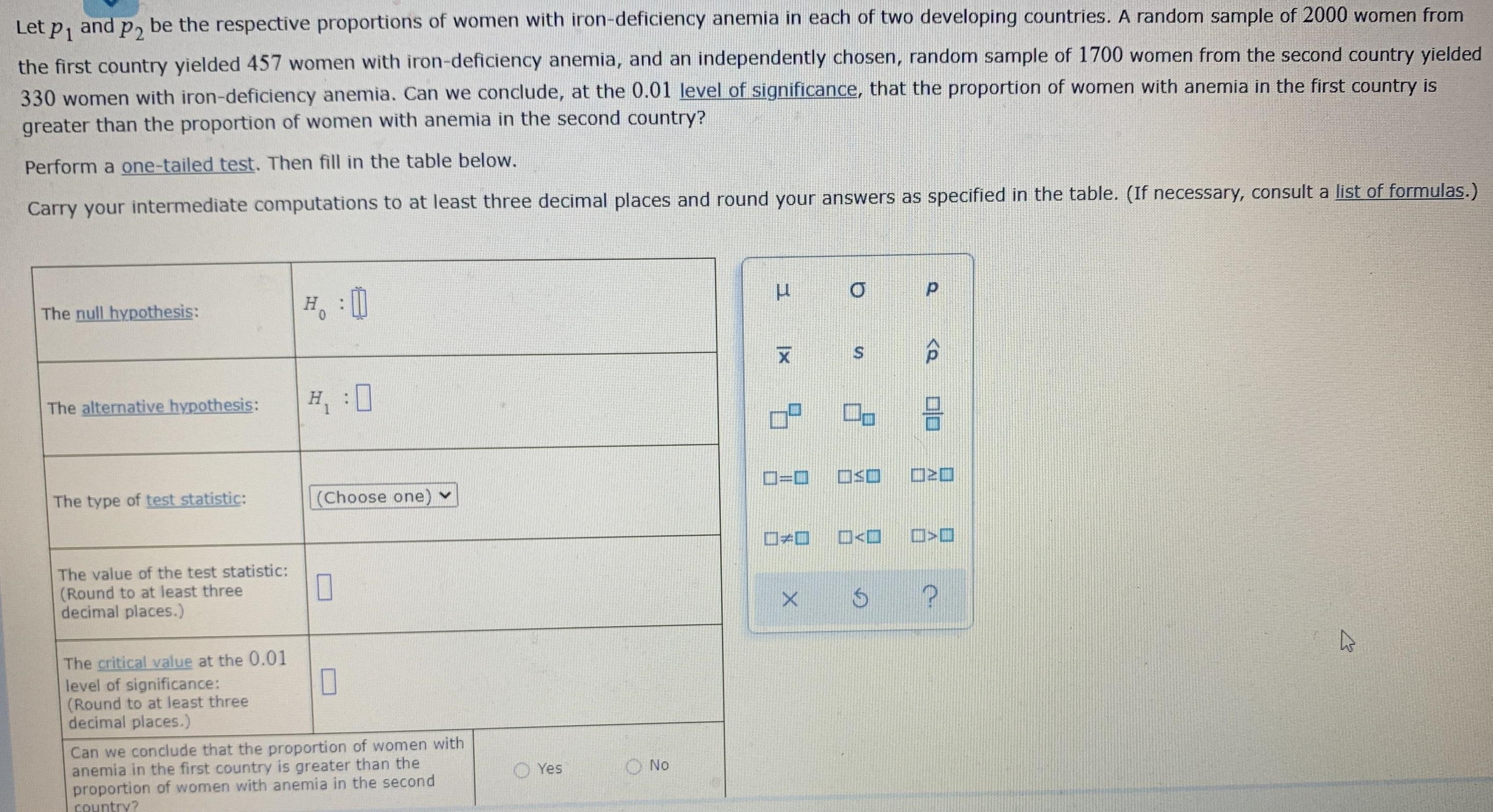
Let P1 and P2 be the respective proportions of women with iron-deficiency anemia in each of two developing countries. A random sample of 2000 women from the first country yielded 457 women with iron-deficiency anemia, and an independently chosen, random sample of 1700 women from the second country yielded 330 women with iron-deficiency anemia. Can we conclude, at the 0.01 level of significance, that the proportion of women with anemia in the first country is greater than the proportion of women with anemia in the second country? Perform a one-tailed test. Then fill in the table below. Carry your intermediate computations to at least three decimal places and round your answers as specified in the table. (If necessary, consult a list of formulas.) O P The null hypothesis: H. : 0 X S The alternative hypothesis: H :0 The type of test statistic: (Choose one) The value of the test statistic: (Round to at least three decimal places.) The critical value at the 0.01 level of significance: 0 (Round to at least three decimal places.) Can we conclude that the proportion of women with anemia in the first country is greater than the proportion of women with anemia in the second country? Yes No =1 0 X 0|0 > $ ?