*/ #include  #include  #include  #include  /* * */ #define SIZE 8 // The size of the two numbers to be multiplied is 8-bit. // Define the prototypes for functions used in the code. short Booth(char *input1, char *input2); char *menu = " " \ "************Please select the following options******************** " \ " * 1. Booth Algorithm. (Lab 4) * " \ " ******************************************************************* " \ " * e. To Exit, Type 'e' * " \ " ******************************************************************* "; // This function is to convert a 8-bit string source (with char '1' or '0' // into an integer number; for example, if input is "11111110", it will return decimal number // -2 ; if input is "00001111", if will return 15 in 8-bit. // This function should be similar to the function you finished in Lab 3, option 2. char convert_binary_to_signed(char *binary) { } // *Lab 4_A*. Write a function to implement Booth's algorithm to multiply // two 8-bit signed binary numbers. The returned result should be as a decimal number. // For example, if input1 is "11111110", input2 is "00001110", the output should be // (-2) * 14 = -28. or 11111111 11100100 (should be a 16-bit binary number) short Booth(char *input1, char *input2) { signed short result = 0; // short is 16-bit result. signed char a = 0; // This is A in the algorithm. signed char q = 0; // This is Q in the algorithm. signed char m = 0; // This is M in the algorithm. char q_minus_one = 0; // This is the bit q_minus_one in algorithm. signed int count = SIZE; // This is size of input. // as we need to shift a and q together, we should assign it to this 16-bit variable to start shifting. signed short a_q = 0; m = convert_binary_to_signed(input1); // initialize Q and M from inputs. q = convert_binary_to_signed(input2); // Now multiplier and multiplicand are one-byte integer numbers. // finish this function to implement input1 * input2 = result // by using Booth's algorithm...... // should implement Booth's algorithm in the following steps. // Step 1. get q0 bit and q_minus_one and and test if that is 10/01/11/00 // Step 2.1: If 10 and 01, perform corresponding operation on A and Q; then // assign a_q and arithmetic shift to right by one bit. // Step 2.2: If 11 and 00, assign a_q and arithmetic shift to right by one bit. // Step 3: Repeat step 1 and 2 for SIZE times. return result; } // Main function int main(void) { char options; // the option should only be a byte char inputA[SIZE+1] = {0}; // 8-bit multiplicand. char inputB[SIZE+1] = {0}; // 8-bit multiplier. short product = 0; // product should be an unsigned number. // system("cls"); // Supposed to clear the screen now. // But not always working in all system. do{ puts(menu); /* prints Memory Simulation */ fflush(stdin); // clear the input buffer before getchar. options = getchar(); switch (options) { case '1': // lab 4_A input two 8-bit binary numbers and // perform multiplication with Booth's algorithm puts("Please input your multiplicand:"); scanf("%s", &inputA[0]); puts("Please input your multiplier:"); scanf("%s", &inputB[0]); product = Booth(inputA, inputB); // call the Booth algorithm to get the result. printf ("The product of %s and %s is: %d ", inputA, inputB, product); continue; case 'e': puts("Code finished, exit now"); return EXIT_SUCCESS; default: puts("Not a valid entry"); continue; } }while (1); }

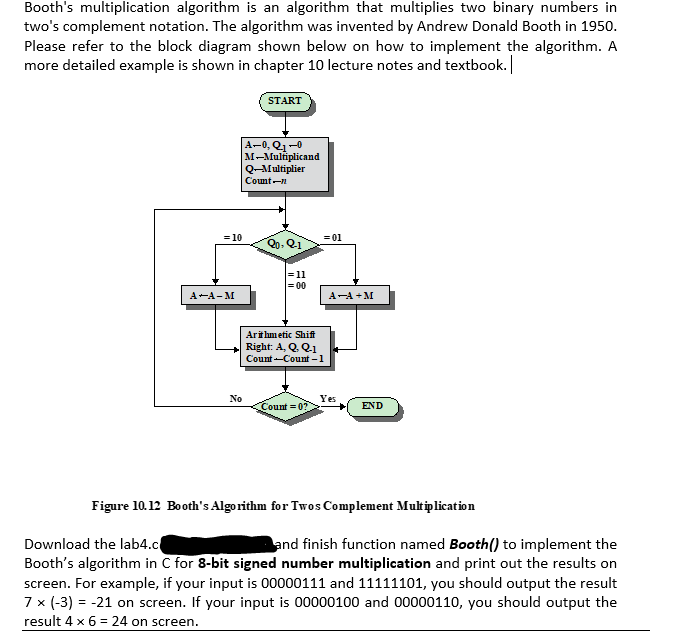
Booth's multiplication algorithm is an algorithm that multiplies two binary numbers in two's complement notation. The algorithm was invented by Andrew Donald Booth in 1950. Please refer to the block diagram shown below on how to implement the algorithm. A more detailed example is shown in chapter 10 lecture notes and textbook. || START A-0, Q10 M-Multiplicand Q-Multiplier Count - = 10 = 01 Qo, Q.1 = 11 = 00 A-A-M AA+M Arithmetic Shift Right: A, QQ-1 Count-Count-1 No Yes Count = 0? END Figure 10.12 Booth's Algorithm for Twos Complement Multiplication Download the lab4.c and finish function named Booth() to implement the Booth's algorithm in C for 8-bit signed number multiplication and print out the results on screen. For example, if your input is 00000111 and 11111101, you should output the result 7 * (-3) = -21 on screen. If your input is 00000100 and 00000110, you should output the result 4 x 6 = 24 on screen. Booth's multiplication algorithm is an algorithm that multiplies two binary numbers in two's complement notation. The algorithm was invented by Andrew Donald Booth in 1950. Please refer to the block diagram shown below on how to implement the algorithm. A more detailed example is shown in chapter 10 lecture notes and textbook. || START A-0, Q10 M-Multiplicand Q-Multiplier Count - = 10 = 01 Qo, Q.1 = 11 = 00 A-A-M AA+M Arithmetic Shift Right: A, QQ-1 Count-Count-1 No Yes Count = 0? END Figure 10.12 Booth's Algorithm for Twos Complement Multiplication Download the lab4.c and finish function named Booth() to implement the Booth's algorithm in C for 8-bit signed number multiplication and print out the results on screen. For example, if your input is 00000111 and 11111101, you should output the result 7 * (-3) = -21 on screen. If your input is 00000100 and 00000110, you should output the result 4 x 6 = 24 on screen