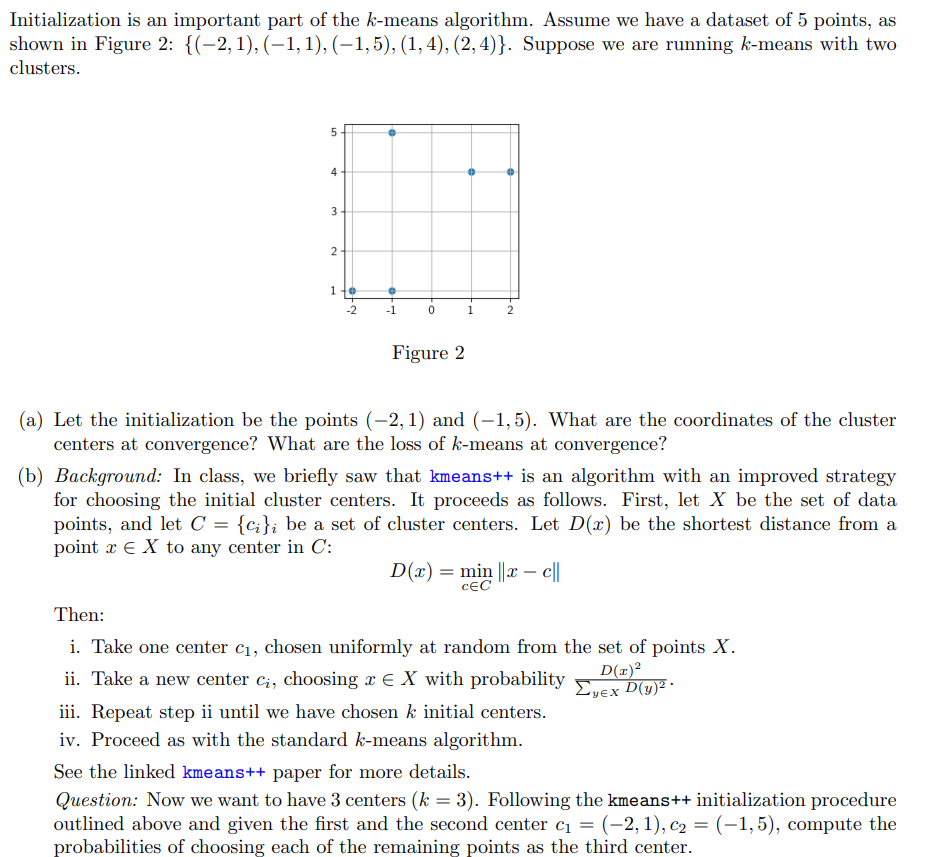
Initialization is an important part of the k-means algorithm. Assume we have a dataset of 5 points, as shown in Figure 2: {(2,1),(1,1),(1,5),(1,4),(2,4)}. Suppose we are running k-means with two clusters. (a) Let the initialization be the points (2,1) and (1,5). What are the coordinates of the cluster centers at convergence? What are the loss of k-means at convergence? (b) Background: In class, we briefly saw that kmeans++ is an algorithm with an improved strategy for choosing the initial cluster centers. It proceeds as follows. First, let X be the set of data points, and let C={ci}i be a set of cluster centers. Let D(x) be the shortest distance from a point xX to any center in C : D(x)=mincCxc Then: i. Take one center c1, chosen uniformly at random from the set of points X. ii. Take a new center ci, choosing xX with probability yXD(y)2D(x)2. iii. Repeat step ii until we have chosen k initial centers. iv. Proceed as with the standard k-means algorithm. See the linked kmeans++ paper for more details. Question: Now we want to have 3 centers (k=3). Following the kmeans++ initialization procedure outlined above and given the first and the second center c1=(2,1),c2=(1,5), compute the probabilities of choosing each of the remaining points as the third center