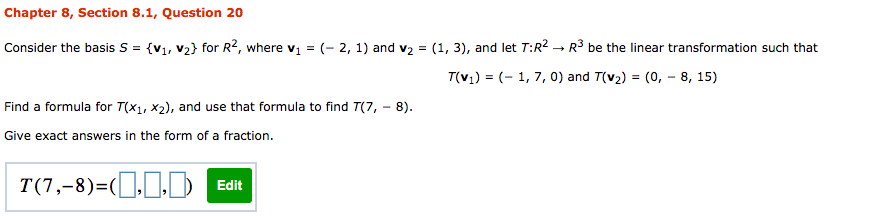
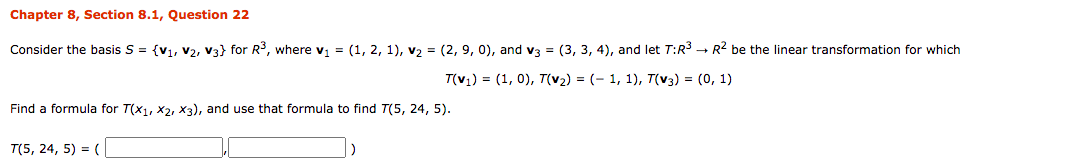
INSTRUCTIONS: ANSWER THE FOLLOWING QUESTION. NO SOLUTION NEEDED AS LONG AS THE FINAL ANSWER IS CORRECT.

1.

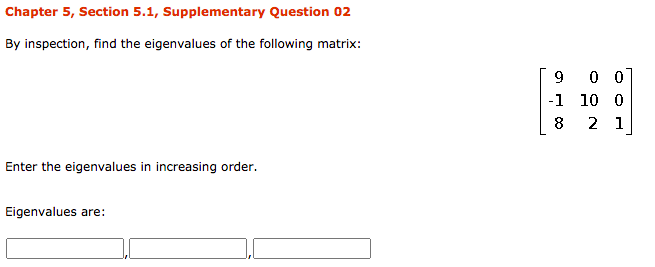
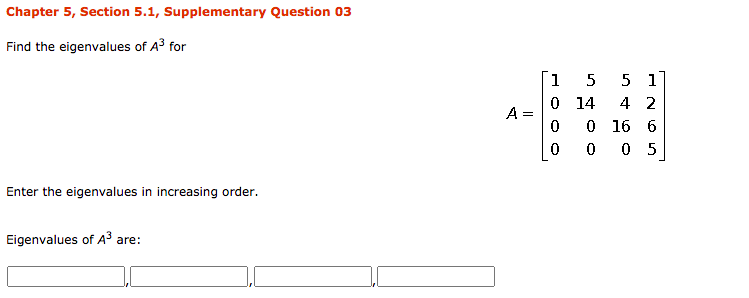
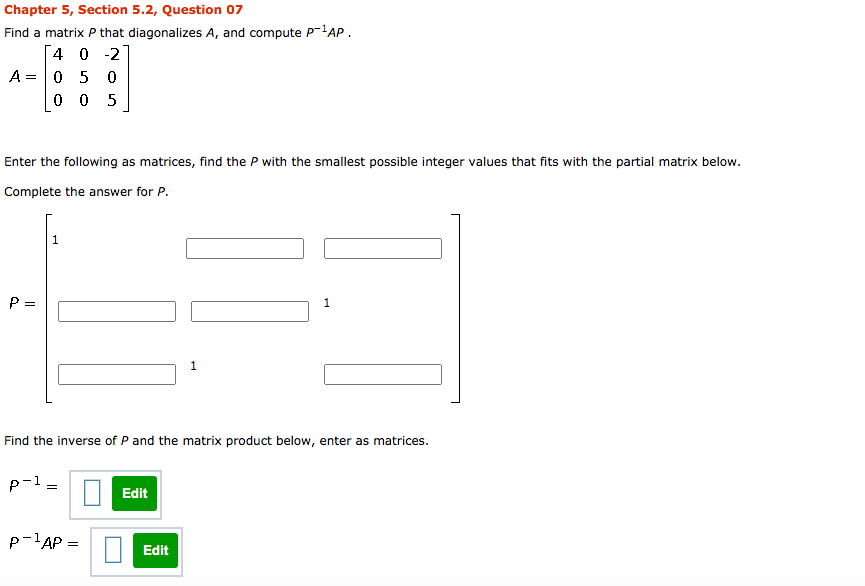
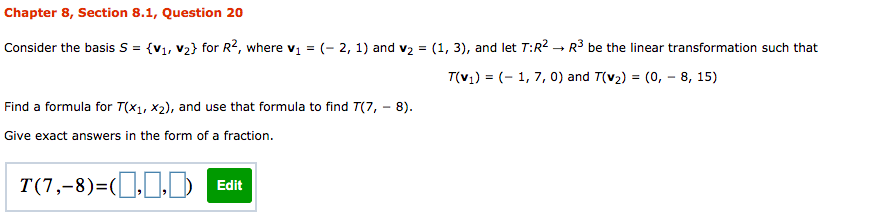
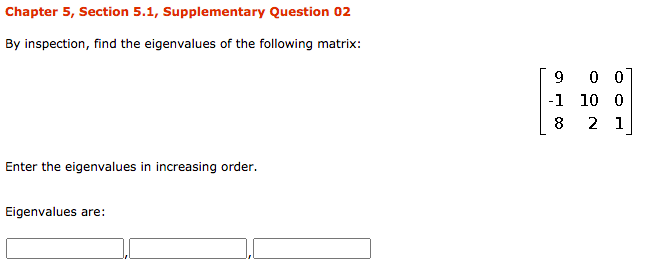
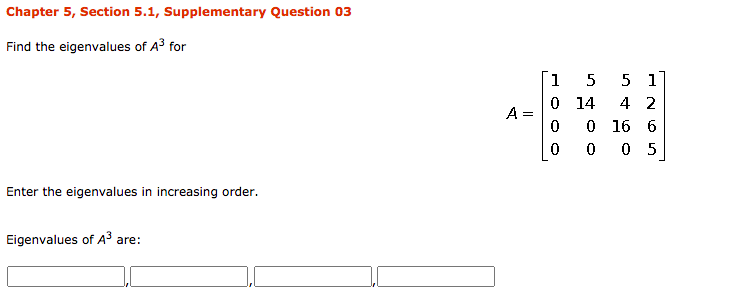
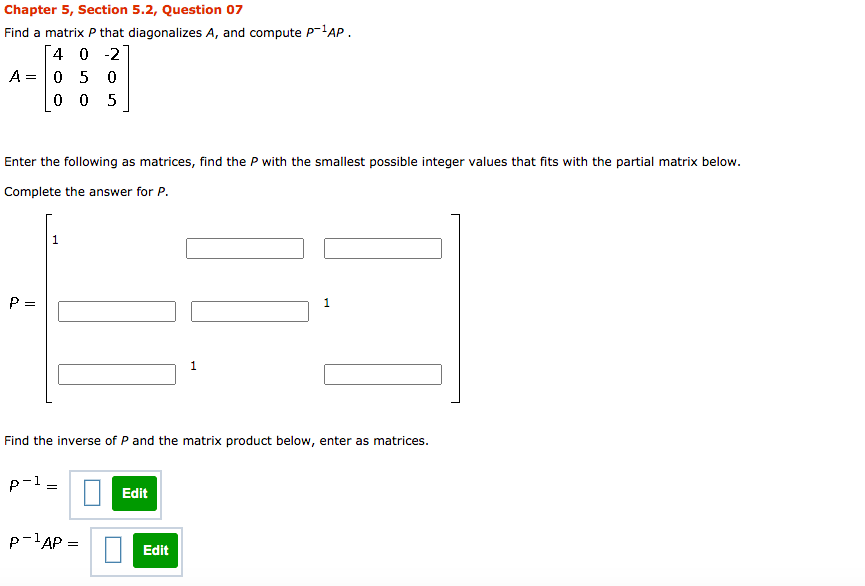
Chapter 5, Section 5.1, Question 24a Find det (A) given that A has p(A) as its characteristic polynomial. P(A) = 13 - 712 + A + 2 det (A) = Hint: See the proof of Theorem 7.1.4. ( If given det (AI - A) = A" + can - + ... + co then, on setting A = 0, det (- A) = cn or (- 1)"det (A) = Cn )Chapter 5, Section 5.1, Supplementary Question 02 By inspection, find the eigenvalues of the following matrix: 9 0 0 -1 10 0 8 21 Enter the eigenvalues in increasing order. Eigenvalues are:Chapter 5, Section 5.1, Supplementary Question 03 Find the eigenvalues of A for 1 5 51 A = 14 4 2 16 6 O U Enter the eigenvalues in increasing order. Eigenvalues of A are:Chapter 5, Section 5.2,. Question 07 Find a matrix P that diagonalizes A, and oompute P'lAP . 4 0 -2 A = 0 5 U U 0 5 Enter the following as matrices, nd the P with the smallest possible integer values that ts with the partial matrix below. Complete the answer for P. 1 E : Find the inverse of P and the matrix product below, enter as matrices. P'lAP2 Em Chapter 5, Supplementary Exercises, Question 15 Find a 3 x 3 matrix A that has eigenvalues A = 0, 8, - 8 with corresponding eigenvectors 1 O 1 H H respectively.Chapter 8, Section 8.1, Question 20 Consider the basis S = {v1, v2} for R4, where v1 = (- 2, 1) and v2 = (1, 3), and let 7:R