Instructions: Answer the following using the R statistical computing platform. Your answer should include the code you wrote plus the output of such code and English rhetoric / coding comments where necessary.

QUESTION: The central term of the binomial random variable is displayed in Example 6.2.5. Suppose you fix a value for and vary from 0 to 1, obtain a plot of against to visualize the "tail" of this distribution

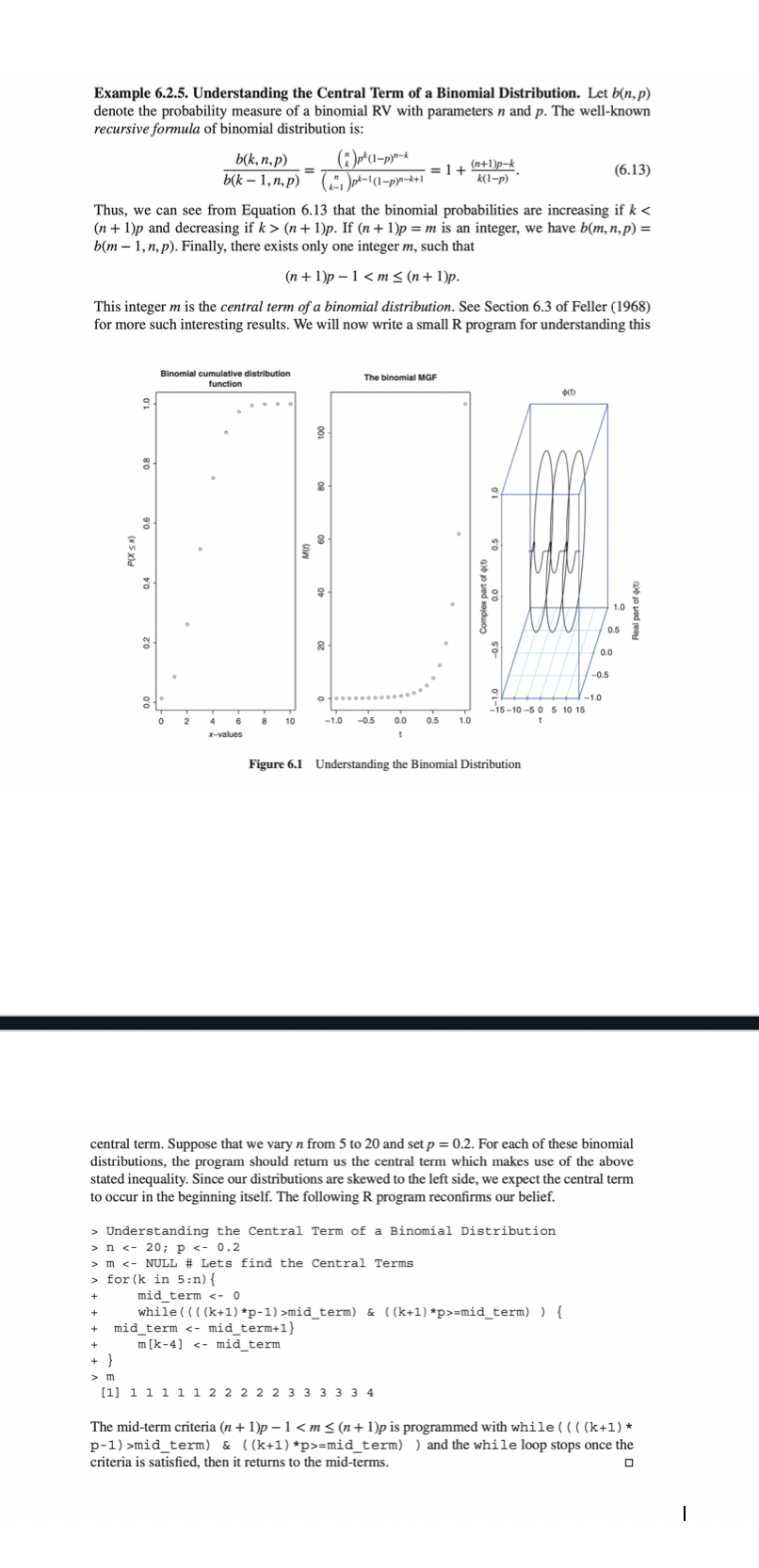
Example 6.2.5. Understanding the Central Term of a Binomial Distribution. Let b(n, p) denote the probability measure of a binomial RV with parameters n and p. The well-known recursive formula of binomial distribution is: b (k, n, p) b(k - 1, n, p) (,", )pt-1(1-p)-4+1 = 1 + ("+Dp-k k(1-p) (6.13) Thus, we can see from Equation 6.13 that the binomial probabilities are increasing if k (n + 1)p. If (n + 1)p = m is an integer, we have b(m, n, p) = b(m - 1, n, p). Finally, there exists only one integer m, such that (n + 1)p - 1 Understanding the Central Term of a Binomial Distribution > n for (k in 5:n) { mid_term mid_term) & ((k+1) *p>=mid_term) ) { mid_term mid_term) & ( (k+1) *p>=mid_term) ) and the while loop stops once the criteria is satisfied, then it returns to the mid-terms