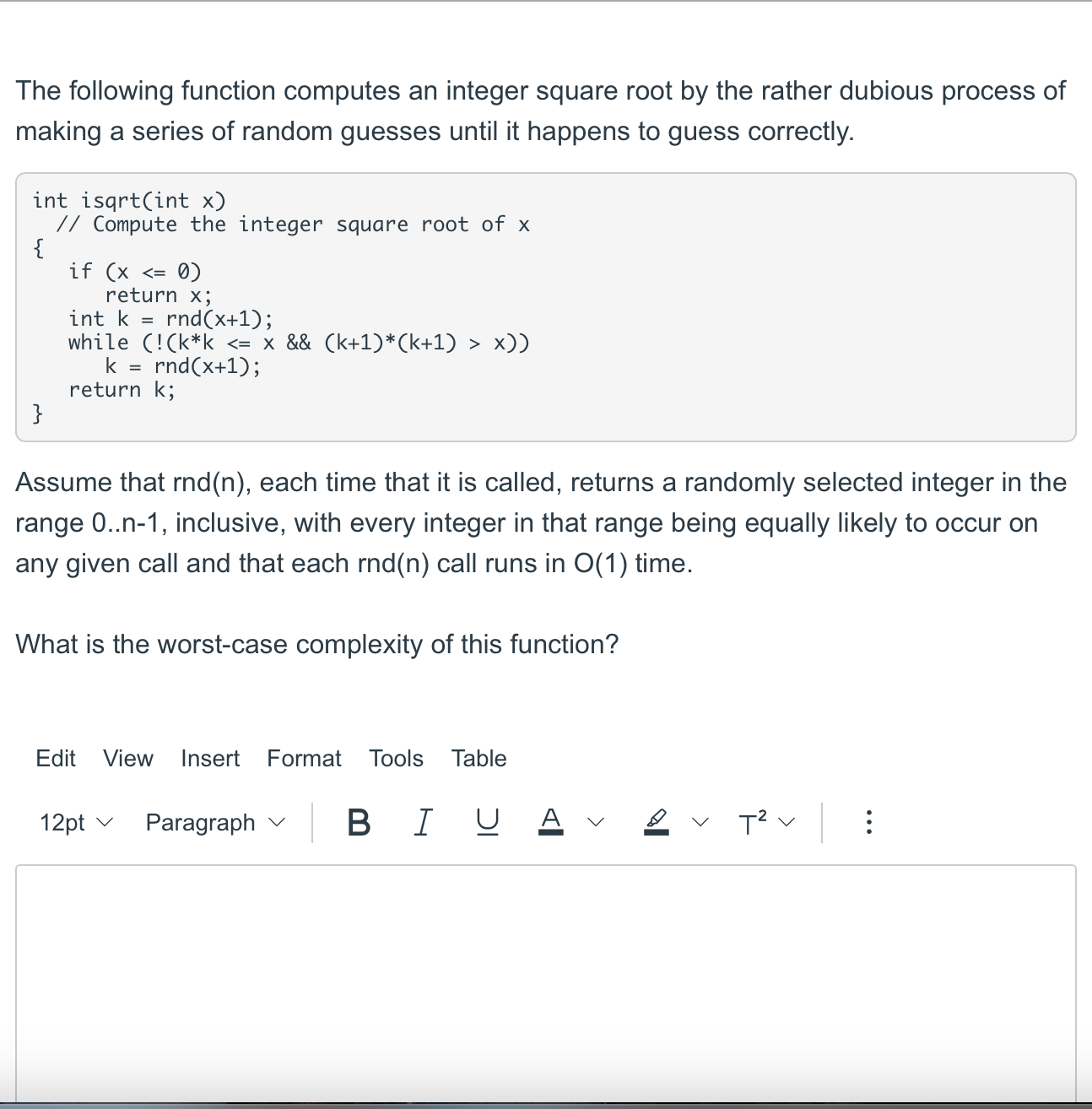
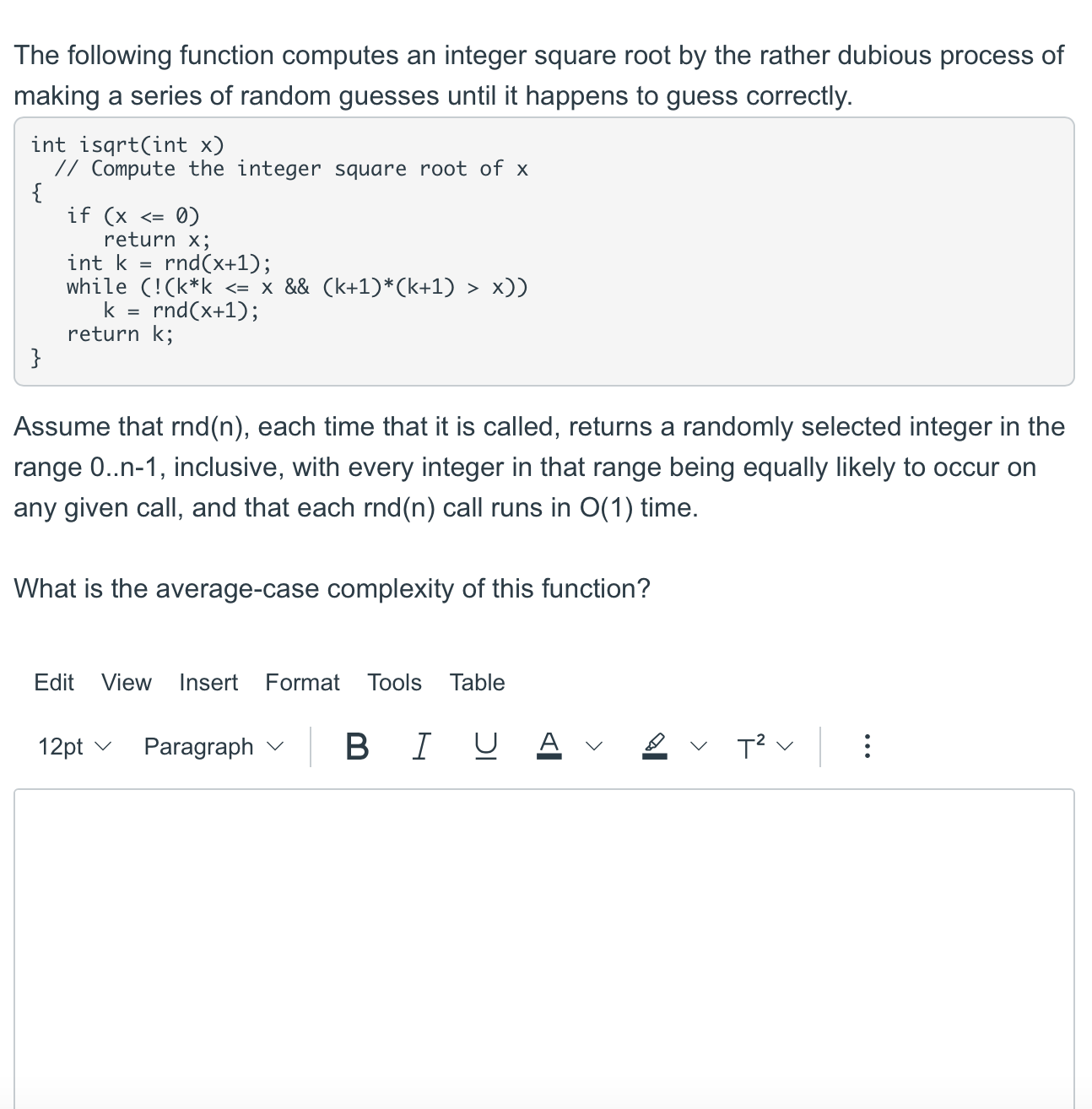
int unordered Search (const T a[], unsigned n, const T& x) // Look for x within an unsorted array a, containing n items. // Return the position where found, or -1 if not found. { } int i; = for (i if (i >= n) i = -1; return i; 0; ((i < n) && (a[i] != x)); i++) ; Suppose that we have arranged the items in our array so that ones most often searched for occur near the beginning of the array. Specifically, assume that: we only search for "x" values that really are in the array "a", and the probability of any particular search being for the element a[i] is c/(2). What is the average case complexity of unordered Search for this input distribution? (Show your work). Edit View Insert Format Tools Table B I U 12pt Paragraph > > T V : The following function computes an integer square root by the rather dubious process of making a series of random guesses until it happens to guess correctly. int isqrt(int x) // Compute the integer square root of x { } if (x The following function computes an integer square root by the rather dubious process of making a series of random guesses until it happens to guess correctly. int isqrt(int x) // Compute the integer square root of x { } if (x