Integer and Non$-$Linear Programming Modeling

Instructions: Answer these questions in MS Excel. All questions require detailed and quantitative solutions.

$1)$ The demand for electricity varies greatly during the day. Because large amounts of electricity cannot be stored economically, electric power companies cannot manufacture electricity and hold it in inventory until it is needed. Instead, power companies must balance the production of power with the demand for power in real time. Most power companies employ meteorologists who constantly monitor weather patterns and update computer models that predict the demand for power over a rolling, $7-$day planning horizon.

$$

Every power company has a base$-$load demand that is relatively constant. To satisfy this base$-$load demand, a power company uses its most economical, low$-$cost power generating assets and keeps them running continuously. To meet additional demands for power above the base$-$load, a power company must dispatch $($or turn on$)$ other generators. These other generators are sometimes called $$peakers$$ as they help the power company meet the highest demands or peak$-$loads. Because different peakers use different types of fuel $($e$.$g$.,$ coal, gas, biomass$),$ their operating costs per megawatt $($MW$)$ generated differ. Thus, dispatchers for a power company continually have to decide which generator to bring online or turn off to meet their load profile in the least costly manner.

$$

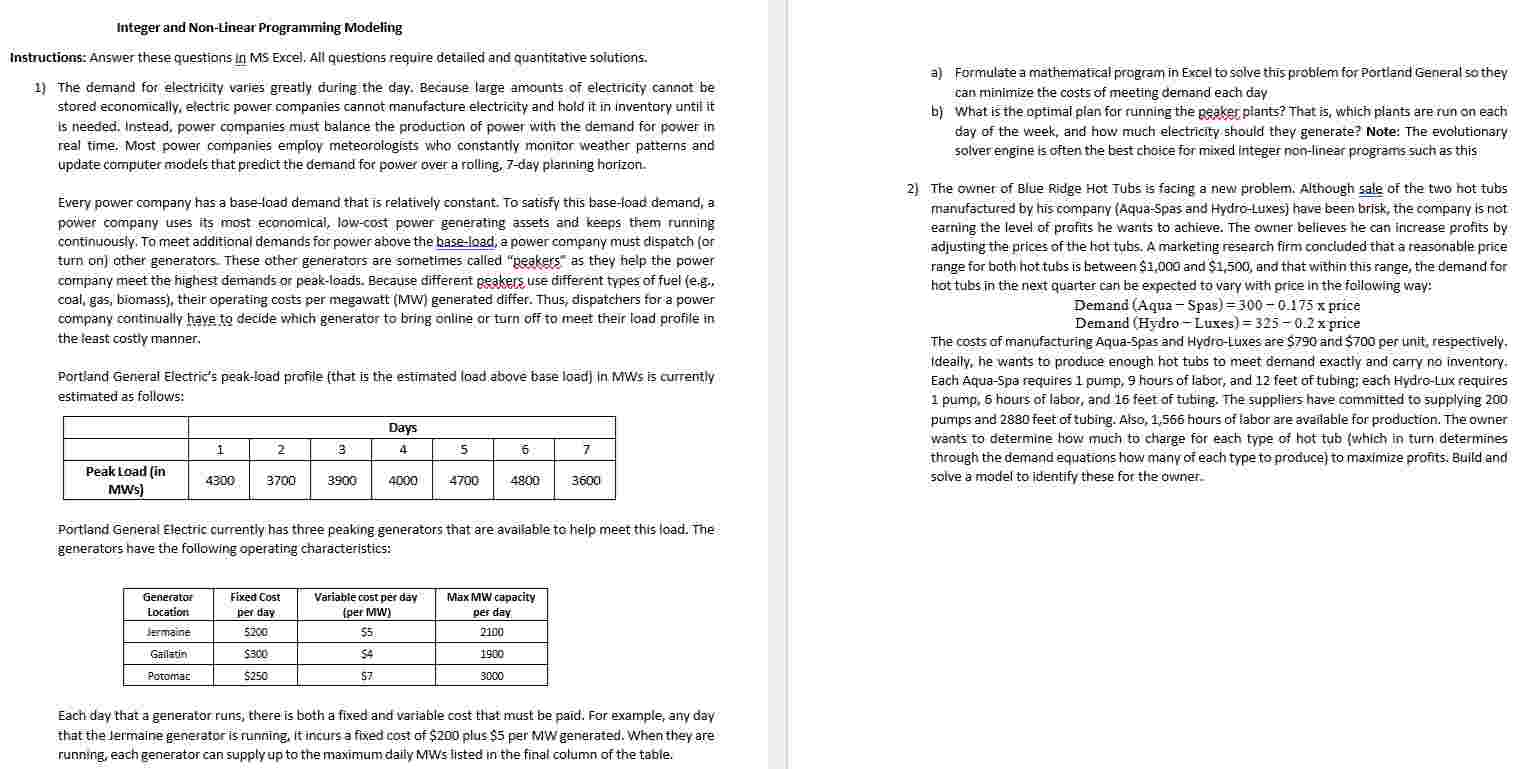
Portland General Electric$$s peak$-$load profile $($that is the estimated load above base load$)$ in MWs is currently estimated as follows:

$$

$$

Days

$$

$1$

$2$

$3$

$4$

$5$

$6$

$7$

Peak Load $($in MWs$)$

$4300$

$3700$

$3900$

$4000$

$4700$

$4800$

$3600$

$$

Portland General Electric currently has three peaking generators that are available to help meet this load. The generators have the following operating characteristics:

$$

Generator Location

Fixed Cost per day

Variable cost per day $($per MW$)$

Max MW capacity per day

Jermaine

$$200$

$$5$

$2100$

Gallatin

$$300$

$$4$

$1900$

Potomac

$$250$

$$7$

$3000$

$$

Each day that a generator runs, there is both a fixed and variable cost that must be paid. For example, any day that the Jermaine generator is running, it incurs a fixed cost of $$200$ plus $$5$ per MW generated. When they are running, each generator can supply up to the maximum daily MWs listed in the final column of the table.

a$)$ Formulate a mathematical program in Excel to solve this problem for Portland General so they can minimize the costs of meeting demand each day

b$)$ What is the optimal plan for running the peaker plants? That is$,$ which plants are run on each day of the week, and how much electricity should they generate? Note: The evolutionary solver engine is often the best choice for mixed integer non$-$linear programs such as this

$$

$2)$ The owner of Blue Ridge Hot Tubs is facing a new problem. Although sale of the two hot tubs manufactured by his company $($Aqua$-$Spas and Hydro$-$Luxes$)$ have been brisk, the company is not earning the level of profits he wants to achieve. The owner believes he can increase profits by adjusting the prices of the hot tubs. A marketing research firm concluded that a reasonable price range for both hot tubs is between $$1,000$ and $$1,500,$ and that within this range, the demand for hot tubs in the next quarter can be expected to vary with price in the following way:

Demand $($Aqua $$ Spas$)=3000\mathrm{.}175$ x price Demand $($Hydro $$ Luxes$)=3250\mathrm{.}2$ x price

The costs of manufacturing Aqua$-$Spas and Hydro$-$Luxes are $$790$ and $$700$ per unit, respectively. Ideally, he wants to produce enough hot tubs to meet demand exactly and carry no inventory. Each Aqua$-$Spa requires $1$ pump, $9$ hours of labor, and $12$ feet of tubing; each Hydro$-$Lux requires $1$ pump, $6$ hours of labor, and $16$ feet of tubing. The suppliers have committed to supplying $200$ pumps and $2880$ feet of tubing. Also, $1,566$ hours of labor are available for production. The owner wants to determine how much to charge for each type of hot tub $($which in turn determines through the demand equations how many of each type to produce$)$ to maximize profits. Build and solve a model to identify these for the owner.