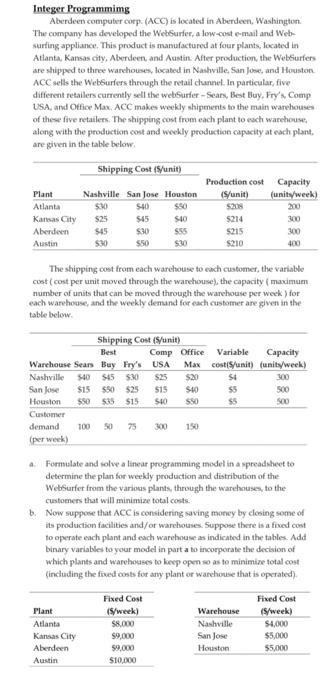
Integer Programmimg Aberdeen computer corp (ACC) is located in Aberdeen, Washington The company has developed the WebSurfer, a low-cost e-mail and Web surfing appliance. This product is manufactured at four plants, located in Atlanta, Kansas city, Aberdeen, and Austin. After production, the WebSurfers are shipped to three warehouses, located in Nashville, San Jose, and Houston ACC sells the WebSurfers through the retail channel. In particular, five different retailers currently sell the webSurfer - Sears, Best Buy, Fry's Comp USA, and Office Max. ACC makes weekly shipments to the main warehouses of these five retailers. The shipping cost from each plant to each warehouse along with the production cost and weekly production capacity at each plant, are given in the table below Shipping Cost (unit) Plant Atlanta Kansas City Aberdeen Austin Nashville San Jose Houston SNO $40 $50 $25 545 $40 SAS $30 S55 530 $50 $30 Production cost (Sunit) 5209 5214 5215 5210 Capacity funity week) 200 300 400 The shipping cost from each warehouse to each customer, the variable cost cost per unit moved through the warehouse), the capacity (maximum number of units that can be moved through the warehouse per week for each warehouse, and the weekly demand for each customer are given in the table below Shipping Cost (unit) Best Comp Office Variable Capacity Warehouse Sears Buy Fry's USA Max cost(S/unit) (units/week) Nashville 540 $45 SNO $25 S20 st 100 San Jose $15 $50 525 515 $40 55 500 Houston 55035515 540 SSO S5 500 Customer demand 100 75 150 (per week) Formulate and solve a linear programming model in a spreadsheet to determine the plan for weekly production and distribution of the WebSurfer from the various plants, through the warehouses, to the customers that will minimize total costs. b. Now suppose that ACC is considering saving money by closing some of its production facilities and/or warehouses. Suppose there is a fixed cost to operate each plant and each warehouse as indicated in the tables. Add binary variables to your model in part a to incorporate the decision of which plants and warehouses to keep open so as to minimize total cost (including the fixed costs for any plant or warehouse that is operated) Plant Atlanta Kansas City Aberdeen Austin Fixed Cost 15/week) $8.000 $9,000 59,000 $10,000 Warehouse Nashville San Jose Houston Fixed Cost (S/week) $4,000 $5,000 $5,000