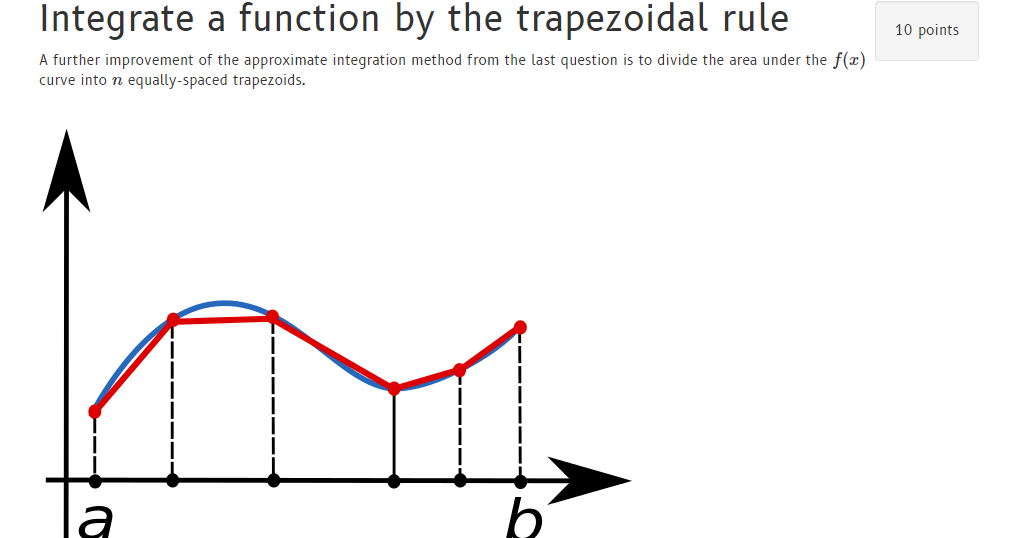
Integrate a function by the trapezoidal rule 10 points A further improvement of the approximate integration method from the last question is to divide the area under the f(x) curve into n equally spaced trapezoids. a Based on this idea, the following formula can be derived for approximating the integral: dx f(x) h (f(x) + f(x+1)), where h is the width of the trapezoids, h = (b-a), and I; = a + ih, i 0,..., n, are the coordinates of the sides of the trapezoids. The figure above visualizes the idea of the trapezoidal rule. Implement this formula in a Python function trapezint[ f, a, b, n ). You may need to check and see if b > a, otherwise you may need to swap the variables. For instance, the result of trapezint( math. sin, 0, 0.5*math. pi, 10 ) should be 0.9979 (with some numerical error). The result of trapezint ( abs, -1, 1, 10 ) should be 1.0. (This assignment is based on Langtangen, Exercise 3.11a.)