Question: Integration - Improper Integrals: Problem 1 (1 point) Determine whether the integral is divergent or convergent. If it is convergent, evaluate it. If it diverges

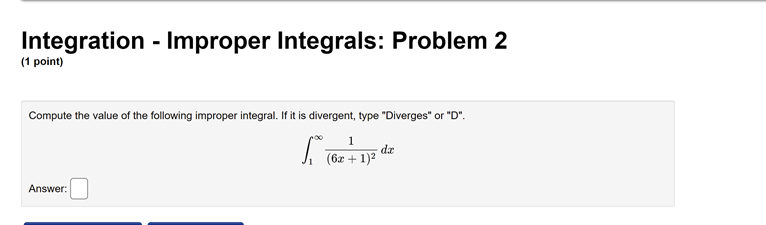
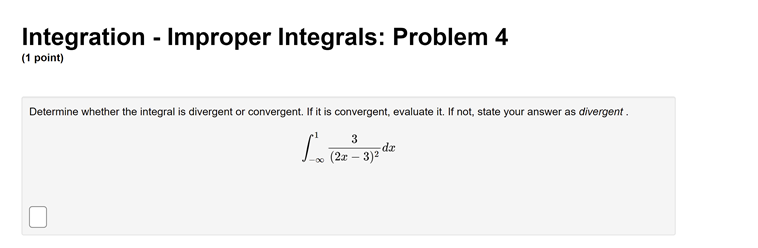
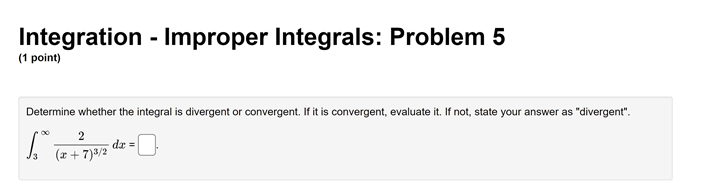
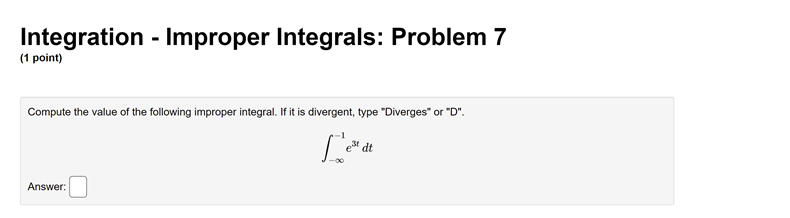
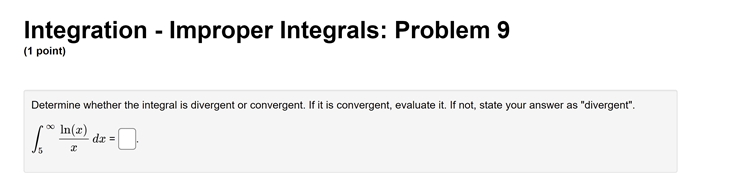
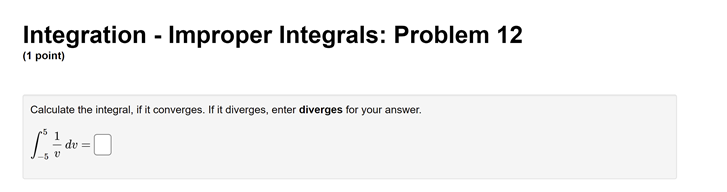
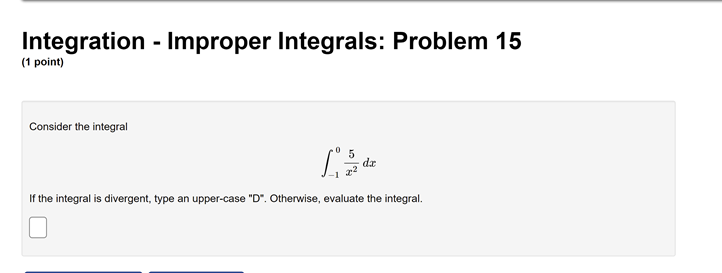
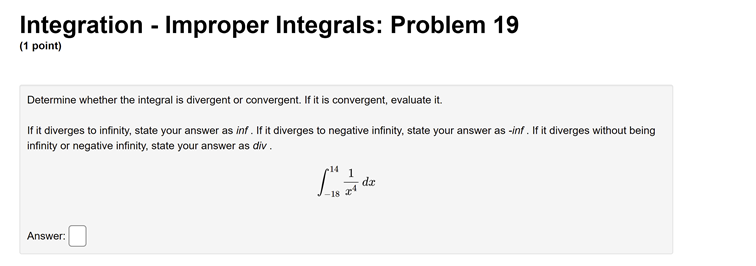
Integration - Improper Integrals: Problem 1 (1 point) Determine whether the integral is divergent or convergent. If it is convergent, evaluate it. If it diverges to infinity, state your answer as INF. If it diverges to negative infinity, state your answer as MINF. If it diverges without being infinity or negative infinity, state your answer as DIV.Integration - Improper Integrals: Problem 2 (1 point) Compute the value of the following improper integral. If it is divergent, type "Diverges" or "D". 1 (6x + 1)2 Answer:Integration - Improper Integrals: Problem 3 (1 point) Determine if the improper integral converges and, if so, evaluate it. Jo 2+5 Write F if the integral doesn't converge.Integration - Improper Integrals: Problem 4 (1 point) Determine whether the integral is divergent or convergent. If it is convergent, evaluate it. If not, state your answer as divergent . 3 (2x - 3)2Integration - Improper Integrals: Problem 5 (1 point) Determine whether the integral is divergent or convergent. If it is convergent, evaluate it. If not, state your answer as "divergent". 2 di = (+ + 7)3/2Integration - Improper Integrals: Problem 6 (1 point) Determine whether the integral is divergent or convergent. If it is convergent, evaluate it. If not, state your answer as "divergent."Integration - Improper Integrals: Problem 7 (1 point) Compute the value of the following improper integral. If it is divergent, type "Diverges" or "D". ell dt Answer:Integration - Improper Integrals: Problem 8 (1 point) Determine whether the integral is divergent or convergent. If it is convergent, evaluate it. If not, state your answer as "divergent." 1 2 + 1Integration - Improper Integrals: Problem 9 (1 point) Determine whether the integral is divergent or convergent. If it is convergent, evaluate it. If not, state your answer as "divergent". In(@)Integration - Improper Integrals: Problem 10 (1 point) Compute the value of the following improper integral. If it is divergent, type "Diverges" or "D". Answer:Integration - Improper Integrals: Problem 11 (1 point) Compute the value of the following improper integral. If it is divergent, type "Diverges" or "D". 8 Answer:Integration - Improper Integrals: Problem 12 (1 point) Calculate the integral, if it converges. If it diverges, enter diverges for your answer. .5 du:Integration - Improper Integrals: Problem 13 (1 point) Determine whether the integral is divergent or convergent. If it is convergent, evaluate it. If it diverges to infinity, state your answer as INF. If it diverges to negative infinity, state your answer as MINF. If it diverges without being infinity or negative infinity, state your answer as DIV.Integration - Improper Integrals: Problem 14 (1 point) Calculate So - Write F if the integral doesn't converge.Integration - Improper Integrals: Problem 15 (1 point) Consider the integral If the integral is divergent, type an upper-case "D". Otherwise, evaluate the integral.Integration - Improper Integrals: Problem 16 (1 point) Consider the integral If the integral is divergent, type an upper-case "D". Otherwise, evaluate the integral.Integration - Improper Integrals: Problem 17 (1 point) Consider the integral g In() If the integral is divergent, type an upper-case "D". Otherwise, evaluate the integral.Integration - Improper Integrals: Problem 18 (1 point) Consider the integral 2 2 If the integral is divergent, type an upper-case "D". Otherwise, evaluate the integral.Integration - Improper Integrals: Problem 19 (1 point) Determine whether the integral is divergent or convergent. If it is convergent, evaluate it. If it diverges to infinity, state your answer as inf . If it diverges to negative infinity, state your answer as -inf . If it diverges without being infinity or negative infinity, state your answer as div . -14 1 -18 74

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Section 6.6: Problem 2 (1 point) Determine whether the integral is divergent or convergent. If it is convergent, evaluate it. If it diverges to infinity, state your answer as INF . If it diverges to...

ANSWER ALL ( FINAL ANSWER ONLY ACCEPTABLE) (1 point) Determine whether the integral is divergent or convergent. If it is convergent, evaluate it. If not, state your answer as "divergent". 00 f L dx =...

calculus 2 Section 6.6: Problem 15 [1 point: In electromagnetic theory, the magnetic potential 1; at a point on the axis of a circular coil is given by \"'3 dz \"=A'fa m 1where A, r, a. are...

(1 point) Determine whether the integral is divergent or convergent. If it is convergent, evaluate it. If it diverges to infinity, state your answer as INF . If it diverges to negative infinity,...

(1 point) Determine whether the integral is divergent or convergent. If it is convergent, evaluate it. If it diverges to infinity, state your answer as "INF" (without the quotation marks). If it...

I need help with these calculus questions: WeBWork 5 - Topics 10 - 12: Problem 4 (1 point) Find the following limit using I'Hopital's Rule: lim So Vt cost dt x-70+ 2 2 Answer: Enter the word...

WeBWorK 5 - Topics 10 - 12: Problem 4 (1 point) dt, then F'(x) = a) If F(x) = = dt, then 23 b) If F(x) = 2 t dt, then F'(x) = t c) If F(x) = Lo 1 dt, then F'(x) = t x+1 1 c) If F(x) = dt, then F'(x)...

\fSection 6.6: Problem 11 (1 point) Determine whether the integral is divergent or convergent. If it is convergent, evaluate it. If not, state your answer as divergent . 3 dx V1 - 22 Preview My...

( 1 point ) Determine whether the integral is divergent or convergent. If it is convergent, evaluate. If not, state your answer as "divergent". 0 9 e xdx 0 9 e xdx =

Donnie Smith Assignment Section 8.1 due 04/17/2017 at 11:59pm MST 5. (1 point) Determine whether the sequence is divergent or convergent. If it is convergent, find the limit. If not, state your...

1. In the following system, where, |201 s +1 1 D(s) = kp G(s)= s2 s+ 12 R(s) o E D(s) G(s) O Y(s) Sketch the root locus with respect to ky for the closed loop system. (include the asymptotus,...

In Problem 13.10 on page 532, you used box office gross to predict DVD revenue (stored in Movie). Using the results of that problem, a. determine the coefficient of determination, r2, and interpret...

EXERCISE 9-18. Calculate the Payback Period The Lower Valley Wheat Cooperative is considering the construction of a new silo. It will cost $41,000 to construct the silo. Determine the payback period...

I want a report about the DOCKERS Creating Sub-Brand current situation something like ppt references are attached ools Window Help B table of contents.pdf (page 230 of 392) Search REFERENCES 1 4 7...

5. Based on your desired future, answer the following questions: (a) What do you want, i.e. what goals have you set yourself? Set up three goals in order of priority. (b) Why do you want this? (c)...

1. Discuss the following statements: (a) Its what you are best at that will be your downfall. (b) How can we learn but not learn? (c) Learning to see is different from seeing. (d) Creativity is...

2. In this chapter, the reader should reflect on the following concepts: The trimming effect, vision, steady course paradox, bottom line, prisoners dilemma, social dilemma, CI strategy, CCI strategy,...