Interfaces

1. What is a Java interface? See S&W page 100 for an example. Note that an interface can have constants as well as methods, so the statement there that an "interface is nothing more than a list of instance methods" is not completely true.
2. Write a Java interface source file UnionFind.java to (as far as possible) express the API on page 219, the union-find API. Also rewrite just the first line of UF.java to assert that class UF implements this interface.
3. What methods/constructors of UF.java, page 221, are not in the interface?
4. Does WeightedQuickUF, page 228, qualify for implementing the interface? Explain why or why not.
5. Please help me nobody this answer post this quetion
6. please help me as soon as possible.
7. Thank You

thank you

i send you all pictures

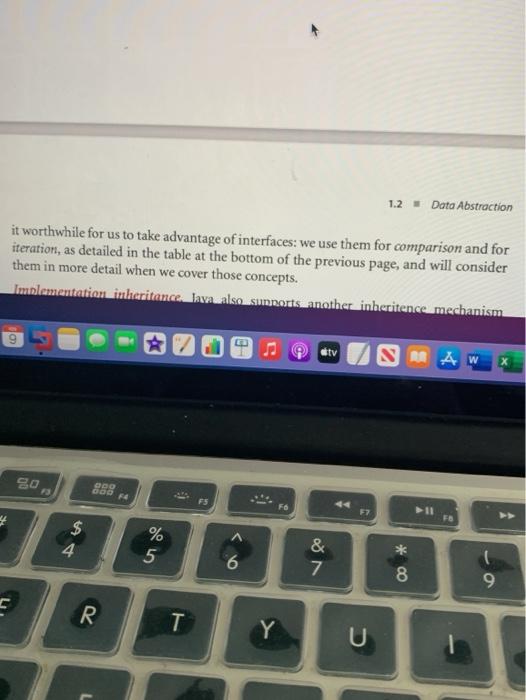
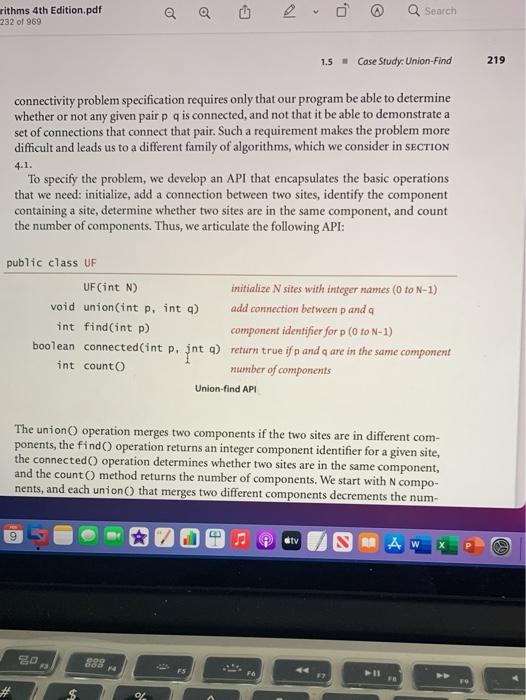
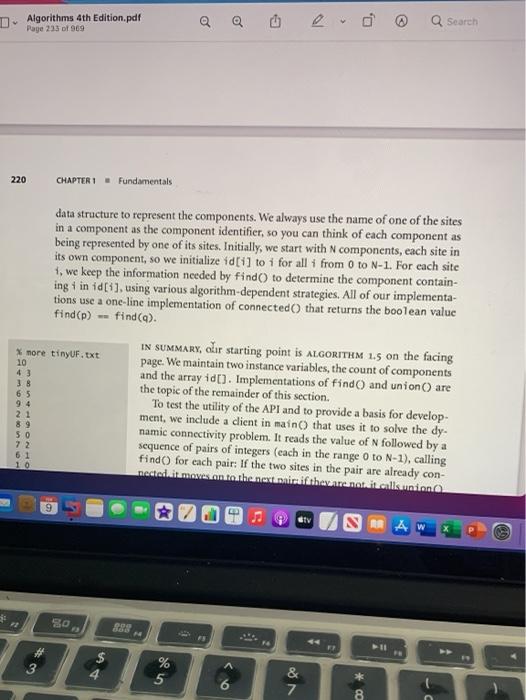
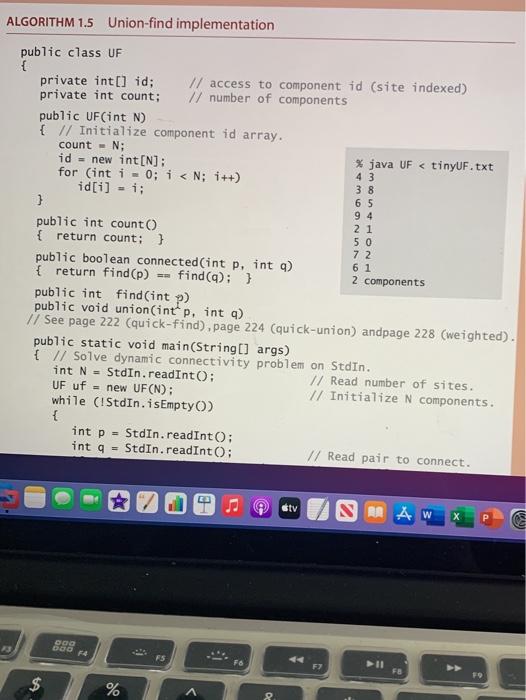
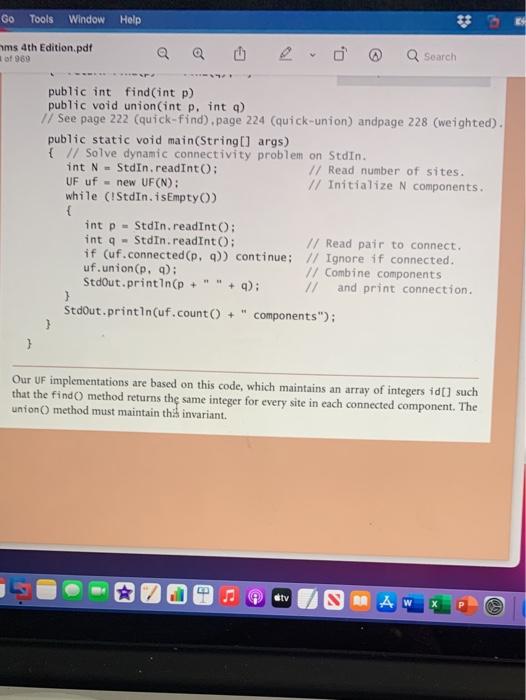
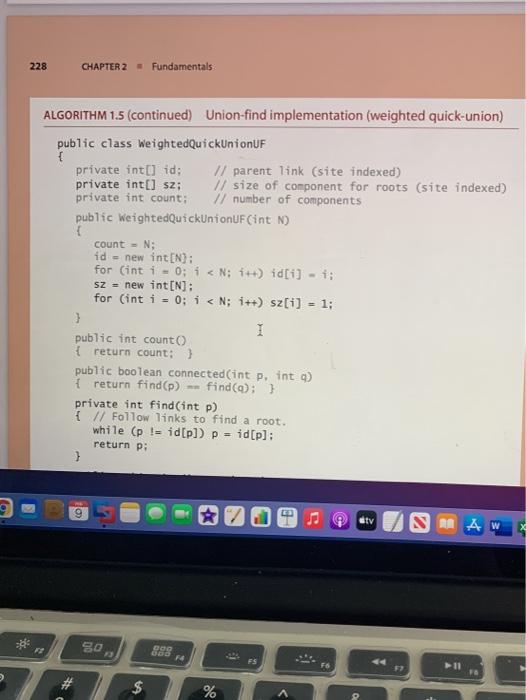
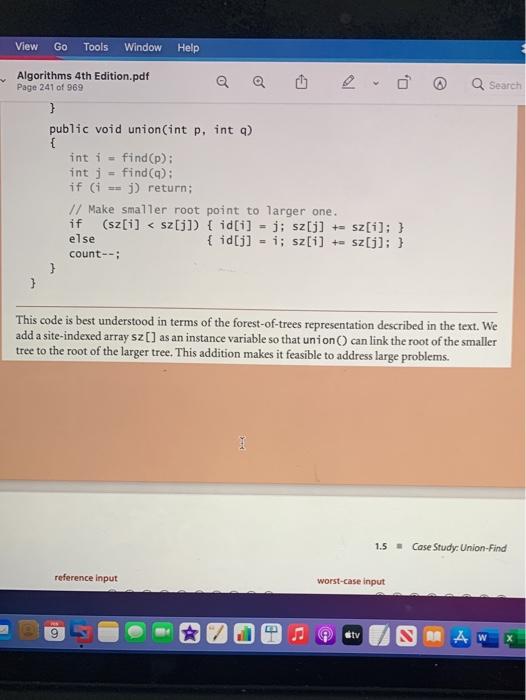
Edit View Go Tools Window Help Algorithms 4th Edition.pdf o Search e Page 113 of 969 100 CHAPTER 1 - Fundamentals Interface inheritance. Java provides language support for defining relationships among objects, known as inheritance. These mechanisms are widely used by software developers, so you will study them in detail if you take a course in software engineer- ing. The first inheritance mechanism that we consider is known as subtyping, which allows us to specify a relationship between otherwise unrelated classes by specifying in an interface a set of common methods that each implementing class must contain. An interface is nothing more than a list of instance methods. For example, instead of using our informal API, we might have articulated an interface for Date: public interface Datable int month 0 : int dayO: int year: } and then referred to the interface in our implementation code public class Date implements Datable { // implementation code (same as before) } so that the Java compiler will check that it matches the interface. Adding the code implements Datable to any class that implements month, day, and year() pro- vides a guarantee to any client that an object of that class can invoke those methods. This arrangement is known as interface inheritancean implementing class inherits the interface. Interface inheritance allows us to write client programs that can manipulate objects of any type that implements interface methods section the interface (even a type to be creat- 9 tv SAMA Q Search Algorithms 4th Edition.pdf Page 113 of 969 2.1 so that the Java compiler will check that it matches the interface. Adding the code implements Datable to any class that implements month, day, and year pro- vides a guarantee to any client that an object of that class can invoke those methods. This arrangement is known as interface inheritance-an implementing class inherits the interface. Interface inheritance allows us to write client programs that can manipulate objects of any type that implements interface methods section the interface (even a type to be creat- java.lang.Comparable compare To ed in the future), by invoking meth- ods in the interface. We might have comparison java.util. Comparator compare used interface inheritance in place of our more informal APIs, but chose not to do so to avoid dependence on java.lang. Iterable iterator specific high-level language mecha- iteration nisms that are not critical to the has Next ulderstanding of algorithms and java.util.Iterator nexto 1.3 remove to avoid the extra baggage of inter- face files. But there are a few situa- Java interfaces used in this book tions where Java conventions make 2.5 9 atv A AW 80 09 FE fe FS >> 1.2 Data Abstraction it worthwhile for us to take advantage of interfaces: we use them for comparison and for iteration, as detailed in the table at the bottom of the previous page, and will consider them in more detail when we cover those concepts. Implementation inheritance lavalso smotanother inheitence mechanism tv SMA W 80 ODO 3 GOD F FS F6 57 FB $ 4 % 5 6 & 7 * 00 9 5 R T Y U rithms 4th Edition.pdf 232 of 969 O, Search 1.5 - Case Study: Union-Find 219 connectivity problem specification requires only that our program be able to determine whether or not any given pair p q is connected, and not that it be able to demonstrate a set of connections that connect that pair. Such a requirement makes the problem more difficult and leads us to a different family of algorithms, which we consider in SECTION To specify the problem, we develop an API that encapsulates the basic operations that we need: initialize, add a connection between two sites, identify the component containing a site, determine whether two sites are in the same component, and count the number of components. Thus, we articulate the following API: 4.1. public class UF UF (int N) initialize N sites with integer names (0 to N-1) void union(int p. int a add connection between panda int find(int p) component identifier for p (o to N-1) boolean connected (int p. jnt q) return true if u and a are in the same component int count number of components Union-find API The union operation merges two components if the two sites are in different com- ponents, the find operation returns an integer component identifier for a given site, the connected operation determines whether two sites are in the same component, and the count() method returns the number of components. We start with N compo- nents, and each union() that merges two different components decrements the num- E otv OD 7 # OL orithms 4th Edition.par 232 of 969 v 0 Q Search Union-find API The union() operation merges two components if the two sites are in different com- ponents, the find() operation returns an integer component identifier for a given site, the connected() operation determines whether two sites are in the same component, and the count() method returns the number of components. We start with N compo- nents, and each union that merges two different components decrements the num- ber of components by 1. As we shall soon see, the development of an algorithmic solution for dynamic con- nectivity thus reduces to the task of developing an implementation of this API. Every implementation has to Define a data structure to represent the known connections Develop efficient union(), find(), connected(), and count() implementa- tions that are based on that data structure As usual, the nature of the data structure has a direct impact on the efficiency of the algorithms, so data structure and algorithm design go hand in hand. The API already specifies the convention that both sites and components will be identified by int val- ues between 0 and N-1, so it makes sense to use a site-indexed array id[] as our basic I stv RAW X 1. Algorithms 4th Edition.pdf Q Search 220 CHAPTER1 Fundamentals data structure to represent the components. We always use the name of one of the sites in a component as the component identifier, so you can think of each component as being represented by one of its sites. Initially, we start with N components, each site in its own component, so we initialize id[i] to i for all 1 from 0 to N-1. For each site 1, we keep the information needed by find to determine the component contain- ing 1 in id[1], using various algorithm-dependent strategies. All of our implementa- tions use a one-line implementation of connected that returns the boolean value find(p) - find(a). IN SUMMARY, Our starting point is ALGORITHM 1.5 on the facing more tiny UF.txt page. We maintain two instance variables, the count of components and the array id[). Implementations of find and union() are the topic of the remainder of this section. To test the utility of the API and to provide a basis for develop- ment, we include a client in main() that uses it to solve the dy namic connectivity problem. It reads the value of N followed by a sequence of pairs of integers (each in the range o to N-1), calling Find for each pair: If the two sites in the pair are already con- necedit mawe.on to the nextimifithevarantitollsten 10 4.3 3.8 65 9.4 2.1 89 50 72 61 10 2 3 % 5 & 7 8 ALGORITHM 1.5 Union-find implementation 65 21 public class UF { private int[] id; // access to component id (site indexed) private int count; // number of components public UF(int N) { // Initialize component id array. count - N; id = new int[N]: % java UF > 1.2 Data Abstraction it worthwhile for us to take advantage of interfaces: we use them for comparison and for iteration, as detailed in the table at the bottom of the previous page, and will consider them in more detail when we cover those concepts. Implementation inheritance lavalso smotanother inheitence mechanism tv SMA W 80 ODO 3 GOD F FS F6 57 FB $ 4 % 5 6 & 7 * 00 9 5 R T Y U rithms 4th Edition.pdf 232 of 969 O, Search 1.5 - Case Study: Union-Find 219 connectivity problem specification requires only that our program be able to determine whether or not any given pair p q is connected, and not that it be able to demonstrate a set of connections that connect that pair. Such a requirement makes the problem more difficult and leads us to a different family of algorithms, which we consider in SECTION To specify the problem, we develop an API that encapsulates the basic operations that we need: initialize, add a connection between two sites, identify the component containing a site, determine whether two sites are in the same component, and count the number of components. Thus, we articulate the following API: 4.1. public class UF UF (int N) initialize N sites with integer names (0 to N-1) void union(int p. int a add connection between panda int find(int p) component identifier for p (o to N-1) boolean connected (int p. jnt q) return true if u and a are in the same component int count number of components Union-find API The union operation merges two components if the two sites are in different com- ponents, the find operation returns an integer component identifier for a given site, the connected operation determines whether two sites are in the same component, and the count() method returns the number of components. We start with N compo- nents, and each union() that merges two different components decrements the num- E otv OD 7 # OL orithms 4th Edition.par 232 of 969 v 0 Q Search Union-find API The union() operation merges two components if the two sites are in different com- ponents, the find() operation returns an integer component identifier for a given site, the connected() operation determines whether two sites are in the same component, and the count() method returns the number of components. We start with N compo- nents, and each union that merges two different components decrements the num- ber of components by 1. As we shall soon see, the development of an algorithmic solution for dynamic con- nectivity thus reduces to the task of developing an implementation of this API. Every implementation has to Define a data structure to represent the known connections Develop efficient union(), find(), connected(), and count() implementa- tions that are based on that data structure As usual, the nature of the data structure has a direct impact on the efficiency of the algorithms, so data structure and algorithm design go hand in hand. The API already specifies the convention that both sites and components will be identified by int val- ues between 0 and N-1, so it makes sense to use a site-indexed array id[] as our basic I stv RAW X 1. Algorithms 4th Edition.pdf Q Search 220 CHAPTER1 Fundamentals data structure to represent the components. We always use the name of one of the sites in a component as the component identifier, so you can think of each component as being represented by one of its sites. Initially, we start with N components, each site in its own component, so we initialize id[i] to i for all 1 from 0 to N-1. For each site 1, we keep the information needed by find to determine the component contain- ing 1 in id[1], using various algorithm-dependent strategies. All of our implementa- tions use a one-line implementation of connected that returns the boolean value find(p) - find(a). IN SUMMARY, Our starting point is ALGORITHM 1.5 on the facing more tiny UF.txt page. We maintain two instance variables, the count of components and the array id[). Implementations of find and union() are the topic of the remainder of this section. To test the utility of the API and to provide a basis for develop- ment, we include a client in main() that uses it to solve the dy namic connectivity problem. It reads the value of N followed by a sequence of pairs of integers (each in the range o to N-1), calling Find for each pair: If the two sites in the pair are already con- necedit mawe.on to the nextimifithevarantitollsten 10 4.3 3.8 65 9.4 2.1 89 50 72 61 10 2 3 % 5 & 7 8 ALGORITHM 1.5 Union-find implementation 65 21 public class UF { private int[] id; // access to component id (site indexed) private int count; // number of components public UF(int N) { // Initialize component id array. count - N; id = new int[N]: % java UF