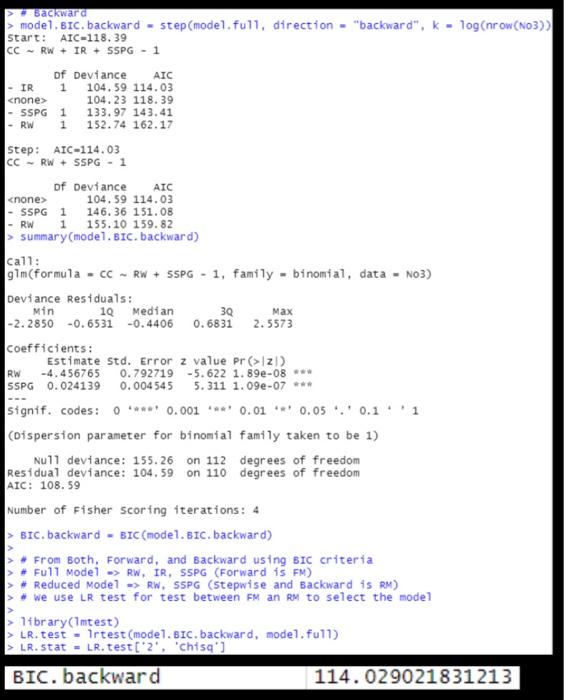
Interpret results from selected model.

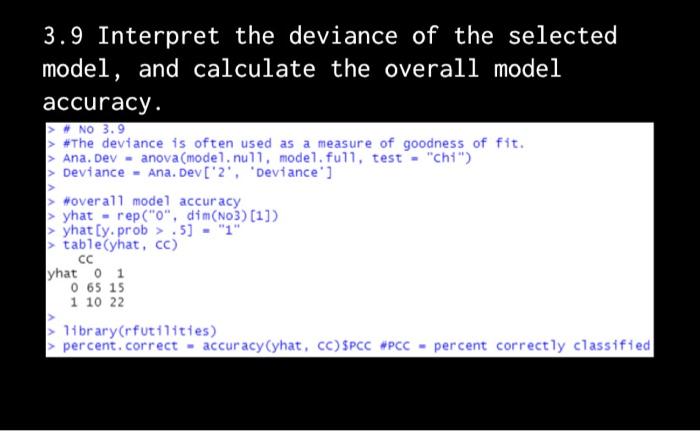
AIC IR RW > Backward model.BIC. backward - step(model.full, direction - "backward", k - log(nrow(N03)) Start: AIC=118. 39 CC - RW + IR + SSPG - 1 Df Deviance 1 104.59 114.03 104.23 118.39 - SSPG 1 133.97 143.41 - RW 1 152.74 162.17 Step: AIC-114.03 CC - RW + SSPG - 1 of Deviance AIC 104.59 114.03 SSPG 1 146.36 151.08 1 155.10 159.82 summary(model. BIC. backward) call: gim(formula - - RW + SSPG - 1, family - binomial, data - N03) Deviance Residuals: Min 10 Median 30 Max -2.2850 -0.6531 -0.4406 0.6831 2.5573 coefficients: Estimate std. Error z value Pr (>Iz) RW -4.456765 0.792719 -5.622 1.89-08 *** SSPG 0.024139 0.004545 5.311 1.09-07 signif. codes: O*** 0.001 0.01 0.05 0.1'1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 155.26 on 112 degrees of freedom Residual deviance: 104.59 on 110 degrees of freedom AIC: 108. 59 Number of Fisher scoring iterations: 4 > BIC. backward - BIC (model. BIC. backward) > From Both, Forward, and Backward using BIC criteria > # Full Model -> RW, IR, SSPG (Forward is FM) Reduced Model > RW. SSPG (stepwise and backward 15 RM) > # we use LR test for test between FM an RM to select the model 1fbrary(Imtest) LR. test - Irtest (model.BIC. backward, model.full) > LR.stat - LR.test('2'. 'chisa'] BIC. backward 114.029021831213 3.9 Interpret the deviance of the selected model, and calculate the overall model accuracy. NO 3.9 > #The deviance is often used as a measure of goodness of fit. > Ana. Dev - anova (model.null, model, full, test - "ch1") > Deviance - Ana. Dev('2', 'Deviance'] > "overall model accuracy yhat - rep "o", dim(NO3) [1]) > yhat[y, prob > .5) - "1" > table (yhat, CC) yhat 01 0 65 15 1 10 22 library(rfutilities) > percent. correct - accuracy(yhat, CC)SPCC #PCC percent correctly classified AIC IR RW > Backward model.BIC. backward - step(model.full, direction - "backward", k - log(nrow(N03)) Start: AIC=118. 39 CC - RW + IR + SSPG - 1 Df Deviance 1 104.59 114.03 104.23 118.39 - SSPG 1 133.97 143.41 - RW 1 152.74 162.17 Step: AIC-114.03 CC - RW + SSPG - 1 of Deviance AIC 104.59 114.03 SSPG 1 146.36 151.08 1 155.10 159.82 summary(model. BIC. backward) call: gim(formula - - RW + SSPG - 1, family - binomial, data - N03) Deviance Residuals: Min 10 Median 30 Max -2.2850 -0.6531 -0.4406 0.6831 2.5573 coefficients: Estimate std. Error z value Pr (>Iz) RW -4.456765 0.792719 -5.622 1.89-08 *** SSPG 0.024139 0.004545 5.311 1.09-07 signif. codes: O*** 0.001 0.01 0.05 0.1'1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 155.26 on 112 degrees of freedom Residual deviance: 104.59 on 110 degrees of freedom AIC: 108. 59 Number of Fisher scoring iterations: 4 > BIC. backward - BIC (model. BIC. backward) > From Both, Forward, and Backward using BIC criteria > # Full Model -> RW, IR, SSPG (Forward is FM) Reduced Model > RW. SSPG (stepwise and backward 15 RM) > # we use LR test for test between FM an RM to select the model 1fbrary(Imtest) LR. test - Irtest (model.BIC. backward, model.full) > LR.stat - LR.test('2'. 'chisa'] BIC. backward 114.029021831213 3.9 Interpret the deviance of the selected model, and calculate the overall model accuracy. NO 3.9 > #The deviance is often used as a measure of goodness of fit. > Ana. Dev - anova (model.null, model, full, test - "ch1") > Deviance - Ana. Dev('2', 'Deviance'] > "overall model accuracy yhat - rep "o", dim(NO3) [1]) > yhat[y, prob > .5) - "1" > table (yhat, CC) yhat 01 0 65 15 1 10 22 library(rfutilities) > percent. correct - accuracy(yhat, CC)SPCC #PCC percent correctly classified